Bonjour Emilie,

suppose que 1) soit vraie, alors comme une boule ouverte est incluse dans la boule fermée correspondante, on a directement 2.

Suppose 2) vraie, et montrons 3).

Par hypothèse, il existe a et r tels que A est inclus dans B'(a,r).
Déjà, on se ramène à une boule ouverte en remarquant qu'on a :

A B'(a,r) B(a,2r).


Soit b un point quelconque fixé de X, il sufit de trouver un autre rayon s tel que :

B(a,2r) B(b,s).

Vois-tu quel s choisir?
Fais intervenir la distance d(a,b).




Pour ton deuxième théorème, remarque que si d et d' sont équivalentes, alors les applications

Id : (E,d) -> (E,d')
x->x


et

Id: (E,d') -> (E,d)
x->x


sont continues, vois-tu pourquoi?


Tigweg

La condition sur s :
d(a,b) + 2r <= s

Sont-elles continues car Id est lipschitzienne ?
Rien ne parle de continuité dans mon cours.
J'ai simplement : Il existe  a,b appartenant à E+ tel que
d<= ad' et d' <= bd
Si d et d' définissent la même topologie, cela veut-il dire que (E,d)=(E,d') ?

Pourriez-vous aussi regarder mes dessins et me dire s'ils sont justes ?
J'ai des problèmes à comprendre l'adhérence et l'intérieur d'un ensemble.

Est-ce une bonne chose de se représenter toutes ces notions géométriquement ?
Sinon, je n'ai pas l'impression de comprendre...

Un grand merci
Emilie.

Un instant je vais m'acheter de quoi déjeuner, je reviens!

Tigweg

Me revoici!
On peut se tutoyer?
Je ne suis pas vieux du tout, et de toute façon, je préfère!


Ok pour les valeurs de s que tu donnes, on a ainsi prouvé 1) => 2) et 2) => 3).

Pour 3) => 4) c'est comme pour 1) => 2) et pour 4) => 1) c'est trivial en incluant B'(a,r) dans B(a,2r) comme on l'a déjà vu, ok pour ce théorème?

Sinon pour l'autre, d'accord aussi avec ce que tu dis:

Dire que d et d' sont équivalentes équivaut à dire que id est lipschitzienne dans les deux cas, en particulier continue.
Pour montrer que les ouverts de d et de d' sont alors les mêmes, donc que (E,d)=(E,d') il suffit de prouver que tout ouvert pour d' est ouvert pour d et inversement.

Soit O un ouvert pour d'.
Ma première application étant continue, qu'en déduis-tu?


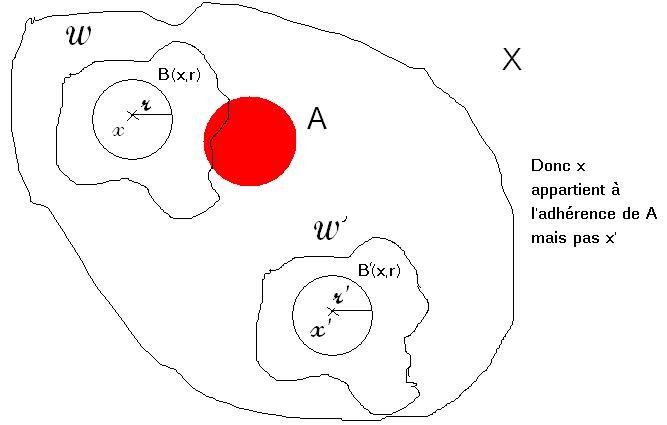
Sinon tes dessins sont faux, x possède un ouvert qui intersecte A mais il y en a d'autres qui ne le rencontreraient pas, il suffit de desssiner l'ouvert moins gros.En fait x et x sont exactement dans le même situation.
x appartiendrait à l'adhérence de A si tout ouvert contenant x rencontrait A, ce qui correspondrait à x dessiné sur la frontière de A (ton cercle) ou à l'intérieur de A (dans ton disque).

C'est une bonne idée de faire des dessins, oui, même si en topologie on ne distingue pas bien des choses un peu subtiles comme l'adhérence de l'intérieur ou l'intérieur de l'adhérence.

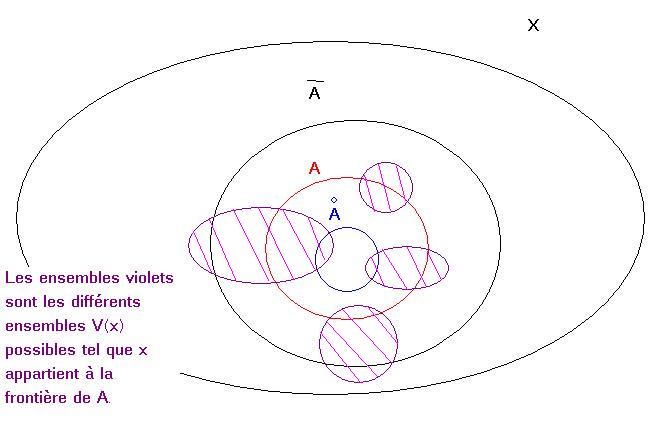
Ton dernier dessin n'a pas de sens, comment parler de V(x) sans dessiner x?
x est dans la frontière de A s'il est sur le "bord de A " encore une fois, et tu peux le visualiser après coup en traçant tous les ouverts que tu veux autour de x, ils rencontreront tous l'intérieur de A et son extérieur.


En espérant que mes explications sont claires!

Tigweg

x et x' sont dans la même situation, pardon!

oui je crois que c'est clair.

donc lorsque d et d' définissent la même topologie, cela veut dire que
(E,d) = (E,d')

car j'ai un exercice où je dois prouver que d'(x,y)=inf {|x-y|, 1}
définit la même topologie que la distance usuelle d sur R mais que d et la distance usuelle sur R ne sont pas équivalentes.
donc faut-il que je prouve que (R, d) = (R, d') ? Seulement je ne sais pas quoi utiliser pour démontrer ça dans la mesure où d et d' ne sont pas équivalentes.

Je voulais aussi te demander si tu étais prof ou passionné des math ou un étudiant brillant.

Emilie.

Bonjour Emilie
Pour répondre à ta question, je suis prof de maths dans le Secondaire!

Sinon quand j'ai écrit (E,d) = (E,d'), c'est uniquement au sens des espaces topologiques, autrement dit que d et d' définissent sur E les mêmes ouverts, sans pour autant que d et d' soient égales.
En fait il est plus exact de dire (E,T) = (E,T') où T et T' sont les topologies de E respectivement définies par d et d'.

Cela dit, le fait que des sistances soient équivalentes implique que les topologies sont les mêmes, mais ce n'est pas une condition nécessaire à cela :

autrement dit, il y a des distances non équivalentes et qui pourtant définissent encore a même topologie sur un espace donné.On dit que 2 distances d et d' sur E sont topologiquement équivalentes si elles défnissent la mm topologie sur E.
C'est le cas danns ton exo, où il faut partir d'un ouvert au sens usuel pour IR et montrer qu'il est aussi ouvert pour d' (tu prends un point a à l'intérieur et tu cherches une boule ouverte de centre a pour la distance d' qui y soit totalement incluse), et vice-versa!

OK?
Bon courage!

Tigweg

Je n'arrive pas à démontrer ça :

Montrer que la distance D(x,y) = inf (|x-y|, 1) définit la même topologie sur R que la distance usuelle sur R.

Voici comment je commence :
Soit V un ouvert sur (R,d) avec d la distance usuelle sur R.
Pour tout a appartenant à V, il existe R > 0 tel que B(a,r) € V.
d et D définissent la même topologie si il existe r'>0 tel que
B(a,r') est inclus dans un ouvert de (R,D),
or D(x,y) = inf (|x-y|, 1) donc
c'est à dire si r'<= 1.

Soit W un ouvert sr (R,D).
d et D définissent la même topologie sur R, si pour tout b € W il existe s>0 tel que B(b,s) est inclus dans un ouvert de (R,d)
or d(x,y) = |x-y|
donc c'est à dire si s = |b-c| avec c un point du bord de B(b,s).

S'il te plaît, pourrais-tu encore un peu m'éclairer ?
Emilie.

Bonjour! .

Je ne suis pas d'accord avec ton premier raisonnement:
en effet, tu dois trouver r' tel que ,x étant un réel fixé, dire que x est dans la boule B(a,r') pour la dstance D entraîne que x est dans la boule B(a,r) pourla distance d.

Cela s'écrit : inf(1,|x-a|) < r' => |x-a| < r.

Or choisir r' < 1 ne garantit pas qu'on aura forcément |x-a| < r puisqu'on ne connaît pas r.
En fait il suffit de choisir r' = inf(1,r) (ou plus petit si tu préfères) pour que cela fonctionne, je te laisse t'en convaincre.

Ainsi V est aussi un ouvert pour D.

Dans l'autre sens, si V est un ouvert pour D, si a en est un point et si r > 0 est tel que la boule (pour D) B(a,r) soit incluse dans V, il s'agit de trouver r'>0 tel que la boule (pour d) B(a,r') soit incluse dans B(a,r), à savoir tel que :


|x-a| < r' => inf(1,|x-a|) < r.

Là encore, le choix r'=inf(1,r) convient.



OK?



Tigweg