Inscription / Connexion Nouveau Sujet
somme des aires de deux carrés
bonjour j'ai un exercice noté à faire et je n'y arrive pas. Pour l'instant, j'ai réussi à faire le a) de la première question mais je bloque pour le reste. Pouriez-vous m'éclairer sur la suite ? Merci.
Voilà le sujet :
[AB] est un segment tel que AB=11 cm ; à partir d'un point M de ce segment, on construit 2 carrés :
..........
........ .
. . .
. . .
A ................. B
M
(objectif : Déterminer s'il existe une position de M telle que la somme des aires des 2 carrés soit 65 cm carré.)
1) les aires dépendent de la position de M sur [AB].posons alors AM=x avec 0<x<11. Il s'agit d'abord d'évaluer la somme dse aires.
a)Prouvez que cette somme est : 2x au carré -22x + 121 (réussi)
b)déduisez en que le problème revient à trouver les solutions del'équation :
x au carré - 11x + 28 = 0
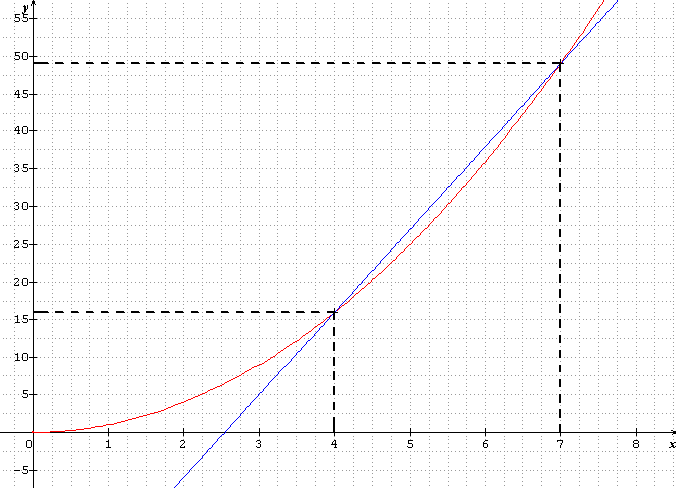
2)on ne sait pas résoudre une telle équation mais elle peut ausi s'écrire x au carré = 11x - 28. d'ou l'idée d'exploiter une représentation graphique de la fonction carré f : x--> x au carré et de la fonction affine g : x-->11x-28 pour conjecturer les solutions.
a) sur quel intervall sont définies les fonctions f et g ?
b)dans un repère orthogonal (O,I,J), en choisissant les unités, tracez leur courbe représentatives.
C) Par lecture graphique vous pouvez obtenir une valeur apprchée des solutions ; prenez leur parties entieres . vérifiez par le calcul que ces entiers sont bien solution.
POUVEZ VOUS M AIDER SVP ?
Edit Coll : espaces… Vérifie avec "Aperçu" avant de poster ! 
je ne sait pas pourquoi ces émoticones rouges se sont affiché. je voulais écrire f : x--> au carré et de l fonction affine g : x ---> 11x-28.
Bonjour . Oui , on peut t'aider, mais il faudrait que tu nous dises ce que tu as fait exactement... Tu as " réussi " la question 1a) et ensuite ...
pour la premiere question j'ai d'abord calculé l'aire du petit carré qui est de x au carré. ensuite celle du 2ème qui est de 121-22x+x au carré.
la somme est donc 2x au carré -22x +121.
je ne comprend pas la question posée ensuite.
D'accord, heureusement qu'on vient de te tracer ces 2 magnifiques courbes ...
Donc tu as ajouté les 2 aires, et on te dit que le total de ces aires est égal à 65. Donc écris le, simplifie, divise par 2, et tu obtiens ...
Merci jacqlouis pour les magnifiques courbes ... 
Il faut surtout remercier l'auteur de Sinequanon pour son mégnifique logiciel ! (d'ailleurs, qui fait partie des membres de l'ile)
Arno, écris que la somme que tu as trouvée est égale au nombre indiqué par l'énoncé, puisqu'on te dit que cette somme des aires doit etre égale à 65 centimètres carrés.
Quand tu auras tout mis au 1er membre, avec 0 au second, tu simplifieras par 2, et tu trouveras ...
merci, je veux bien essayer mais quel "premier membre"?

Bonjour Jamo. Oui, c'est facile pour lui, de trouver les réponses, quand on les lui fournit toutes cuites.
Moi, je voulais, depuis le début, qu'il trouve les solutions... Chacun sa pédagogie ...
Je suis tout à fait d'accord qu'il vaut mieux guider que de donner les solutions, c'est ce que je m'efforce de faire ...
Mais parfois, donner le début vaut mieux qu'un long bla-bla quand on voit que ça coince vraiment trop