Inscription / Connexion Nouveau Sujet
TD mathématiques
Bonjour,
N'ayant pu assister au cours concernant l'essence du TD ci-dessous, j'aurais voulu savoir s'il était possible que vous me donniez des éléments de réponse à ces questions:
D'avance merci!
***************************************************************
1)On considère les fonctions:
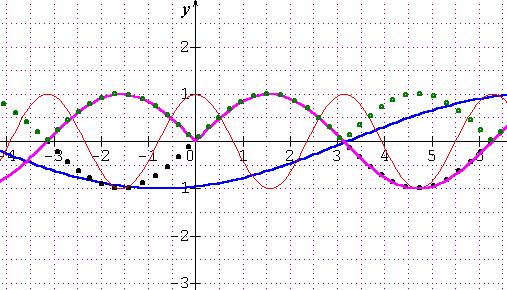
a)f(x)=sin x
b)f(x)= cos(2x)
c)f(x)= sin |x|
d)f(x)= |sin x|
e)f(x)= sin((2
/5)x+5)
Q1>>Quelles sont les fonctions qui n'admettent pas 2 comme periode?
Q2>>Quelle est celle, si elle existe, qui n'est pas périodique?
2)a)Calculer la dérivée logarithmique de la fonction suivante:
f(x)=[(2(x-5))/(x+3)]
(x2+1)
b)Donner les valeurs de x pour lesquelles f'(x) s'annule
NB: Pour indication il est demandé au préalable de déduire f'(x) et de calculer f'(0) et f'(1).
******************************************************************
Merci pour ta réponse
Juste une précision...
**Qu'est-ce qu'une dérivée logarithmique?
De nouveau, merci!
Donc, pour iullustrer, que donnerait la dérivée logarithmique de
f(x)=[(2(x-5))/(x+3)](x2+1)?
Merci...
Bonjour
Commence par prouver que la dérivée logarithmique de fmgn vaut
si m et n sont des entiers relatifs.
Bonjour,
Pouvez-vous me donner la dérivée logarithmique de la fonction suivante?
f(x)=[(2(x-5))/(x+3)](x2+1)
Merci!
*** message déplacé ***
UDCPP :
Si tu penses que ton exercice est parti dans les profondeurs du forum, poste un petit message dans ton topic, il remontera parmi les premiers.
Merci
Désolé que ma demande soit passée pour du multi-post mais ma démarche n'était pas telle. Lorsque j'ai posé ma question pour la première fois, on m'a juste donné d'excellentes indications de réponse; mais débutant dans ce chapitre, je n'arrive pas à m'y retrouver malgré les conseils. J'aurais donc aimé que l'on me "fasse" le calcul afin d'avoir un exemple concret...D'où ma question d'aujourd'hui.
Espérant une réponse, salutations! 
Annuler
connectez vous
analyse en post-bac