Annuler
connectez vous
- Bissectrice et cercle inscrit dans un triangle - Cours 4ème
- Exercice Bissectrices et cercles inscrits dans un triangle
- Cours sur les Figures planes, Distance d'un point à une droite et Tangente à un cercle
- QCM : Figures planes, distance et tangente - Exercice 4ème
- Six Exercices de géométrie pure - quatrième
Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques Collège cycles 3 /4On parle exclusivement de maths, niveau collège. QuatrièmeForum de quatrième GéométrieTopics traitant de géométrie [tout]Lister tous les topics de mathématiques
Niveau quatrième
Déduire qu'une droite est tangente a un cercle.
Posté par VampireRain
Bonjour ! J'ai un petit problème avec mon DM de Maths de cette semaine.
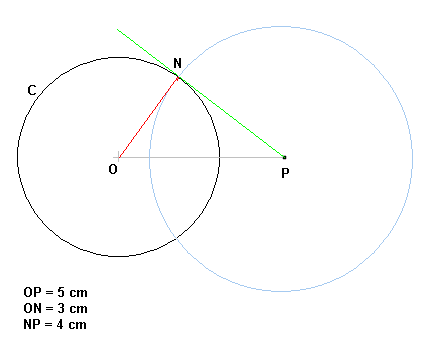
J'ai un cercle C de centre O et de rayon 3cm.
Je dois tracer un triangle soit (OP)=5cm et (PN)=4cm
Je dois ensuite démontrer qu'il est rectangle, ceci est fait il est donc rectangle en O mais je bloque donc sur la consigne suivante :
"En déduire que (PN) est tangente au cercle C"
Si vous pouviez m'aider,
Merci d'avance,
L.
Bonjour,
Es-tu vraiment sûr que le triangle est rectangle en O ? Je le vois plutôt rectangle en N, moi... D'où le fait, d'ailleurs, que (PN) et (ON) soient perpendiculaires, et donc que (PN) soit tangente au cercle puisque perpendiculaire à un rayon. 
Ha oui. J'ai du faire une erreur, j'ai utilisé le théorème suivant :
"Si on joint les point d'un cercela au extémité d'un de ses diamètres alors on obtient un triangle rectangle en ce point"
Même en utilisant ce théorème, tu ne devrais pas montrer qu'il est rectangle en O puisque O est le centre du cercle... De toute façon, tu ne peux même pas l'utiliser ici car P ne peut appartenir à C.
Par contre, en 4e, on voit la réciproque de Pythagore, non ? 
Oui j'ai fait aussi une erreur dans la figure. Voila j'ai refait mais je doit déduire je n'est donc aucune mesure donc je ne peut pas faire pythagore :S
Oups excuse ma débiliter, j'ai des mesures --'.
Je fait le théorème de pythagore, puis sa réciproque =]
Merci de m'avoir remis dans le bon chemin ^^'.
L.
Tu n'as vraiment aucune mesure ? 
Citation :
J'ai un cercle C de centre O et de rayon 3cm.
Je dois tracer un triangle soit OP=5cm et PN=4cm
J'ai un cercle C de centre O et de rayon 3cm.
Je dois tracer un triangle soit OP=5cm et PN=4cm
D'ailleurs, tu sais d'emblée qu'il est rectangle: c'est le fameux cas du triangle 3-4-5 (un des nombreux triplets pythagoriciens) !
Ton énoncé n'est pas complet.
Je suppose (mais cela devrait être dit dans l'énoncé) que N est un point du cercle C.
Si c'est le cas, alors on a ceci :
Calcule :
OP² = ...
NP² = ...
ON² = ...
Et puis pense à Pythagore ...
Oui, car il y a le problème qu'il n'est pas encore démontrer qu'il est rectangle alors que je besoin de le s'avoir pour faire pythagore, je n'ai donc pas besoin de le démontrer je peut calculer totu de suite pythagore et ensuite rajouter la démonstration avec sa réciproque ?
Tu n'as pas besoin de savoir que le triangle est rectangle pour appliquer la réciproque de Pythagore, puisque c'est ce que tu veux démontrer...
Salut J-P
Oui c'est bon =D !
Merci J-P de m'avoir rappeller que j'avais la mesure du rayon =P.
Merci de votre aide. =]
A bientôt !
L.
bonjour
une fois qu'on a établi que l'angle ONP est droit, on sait que (PN) est tangente au cercle C :
la droite perpendiculaire à l'extrémité d'un rayon d'un cercle est tangente à ce cercle
Par contre (excuser moi >.<), j'ai toujours un problème pour déduire que (PN) est tangente au cercle C =/.
bonjour VampireRain
tout point de (NP) autre que N est extérieur au cercle
soit M un de ces points : dans le triangle rectangle ONM, OM est l'hypoténuse et est plus grande que le côté ON qui est le rayon du cercle; M est donc à l'extérieur du cercle