Inscription / Connexion Nouveau Sujet
Algebre et Géométrie différentielle
Bonsoir tout le monde,
voici un petit exo...
On considere
1)Montrer que
Quelle est sa dimension?
2)Montrer que l'application
est
Calculer sa différentielle.
3)Montrer que
En déduire que
Quelle est sa dimension?
>alors je bute dés la premiere question,je pensais comme d'habitude faire intervenir la fonction (de la question 2)
et montrer que c'est une submersion,mais vu que c'est demander ensuite,je crois que je fais fausse route
Et là pour montrer que c'est une sous-variété...je suis bien embêté, quelle est la méthode?
Merci d'avance
Salut robby3! 
Encore une fois je ne connais rien à la géo diff, mais d'après ce que Camélia t'avait répondu dans un fil précédent, je te propose ceci pour la question 1, sans aucune garantie bien sûr:
1)S(n,R) a pour équation dans M(n,R), où l'on note
.
Or g est une application linéaire, donc différentiable en tout point M de M(n,R).
Donc il y a un plan tangent à S(n,R) en tout M de S(n,R).
Je crois avoir compris que cela suffit à prouver que S(n,R) est une sous-variété de M(n,R).
En tout M de S(n,R), le rang de la différentielle , qui n'est autre que g, est égal à
Sa dimension est égale à
A confirmer!
J'espère n'avoir pas raconté trop de bêtises...
En particulier je n'ai pas parlé de submersion, peut-être le faut-il.
Bonjour robby3
1) Bravo Tigweg! En fait ici pour S(n,R) c'est inutile de passer par la théorie différentielle. La fonction g que tu donnes est linéaire, S(n,R)=Ker g; S(n,r) est donc un sous-espace vectoriel qui est l'espèce la plus évidente de sous-variété. Sa dimension est bien n(n+1)/2.
2) Je me conforme à l'énoncé, donc je pose g(M)=MtM-Id. C'est une composée de l'application linéaire M
(M,tM) et de la multiplication qui est bilinéaire. De plus, on voit facilement que g est à valeurs dans S(n,R) et que si M est dans O(n,R), M est inversible.
Commençons par dg_I: Il est clair que Ker(dg_I) est le sous-espace formé des matrices antisymétriques. qui est de dimension n(n-1)/2.
Ensuite pour M dans O(n,R) on voit que H est dans Ker(dg_M) si et seulement HtM=HM-1 est antisymétriqua, donc Ker dg_M est isomorphe aux antisymétriques, et de même dimension n(n-1)/2. Donc dg_M a toujours le même rang.
Récapitulons: g:G(n,R)
S(n,R) et O(n,R)=g^{-1}(0). g est de rang constant n(n+1)/2, donc O(n,R) est une sous-variété de dimension n2-n(n+1)/2=n(n-1)/2
Salut Camélia et merci!
S(n,R)=Ker g; S(n,r) est donc un sous-espace vectoriel qui est l'espèce la plus évidente de sous-variété.
Ok, c'est vrai que j'aurais pu m'en douter!
Bonjour tout les deux!
malgré vos réponses et je vous en remercie...j'aimerais bien comprendre
Alors tout d'abord,d'ou sort ta fonction Tigweg?
On est d'accord que ??
A partir de là pourquoi à pour équation
??
2) Je me conforme à l'énoncé, donc je pose g(M)=MtM-Id. C'est une composée de l'application linéaire M(M,tM) et de la multiplication qui est bilinéaire. De plus, on voit facilement que g est à valeurs dans S(n,R) et que si M est dans O(n,R), M est inversible.
Commençons par dg_I: Il est clair que Ker(dg_I) est le sous-espace formé des matrices antisymétriques. qui est de dimension n(n-1)/2.
Ensuite pour M dans O(n,R) on voit que H est dans Ker(dg_M) si et seulement HtM=HM-1 est antisymétriqua, donc Ker dg_M est isomorphe aux antisymétriques, et de même dimension n(n-1)/2. Donc dg_M a toujours le même rang.
Récapitulons: g:G(n,R)S(n,R) et O(n,R)=g^{-1}(0). g est de rang constant n(n+1)/2, donc O(n,R) est une sous-variété de dimension n2-n(n+1)/2=n(n-1)/2
>Alors là!
j'ai pleins de questions!
je comprend pas Ker(dg_I)...
ou montre t-on que g est une submersion?
Désolé mais j'ai beaucoup de mal là!
Salut robby!
On est d'accord que
->Ca commence mal, tu confonds avec le groupe spécial linéaire!
Il s'agit juste ici des matrices symétriques M, donc qui sont égales à leur transposée, autrement dit telles que g(M)=0.
ah mince!!
j'ai confondu avec un autre sujet!!
bon tans pis on va faire celui que tu as pris
(on fera l'autre plus tard
)
donc en fait je suis d'accord mais ça
Donc il y a un plan tangent à S(n,R) en tout M de S(n,R).
>pourquoi?c'est parce que g est différentiable partout sa différentielle est elle-meme?
Pourquoi ça suffit à dire que c'est une sous-variété?
l'application g va de M(n,R)dans quoi?
g va de Mn(R) dans lui-même.
Pour tes autres questions, je vais modestement m'en remettre à Camélia.
je passe une annonce
Si Kaiser vois mon topic égaré ce soir, qu'il n'hésite pas à venir me secourir
parce que je crois que Camélia ne reviens que demain dans l'aprés midi.
je vais y réfléchir ce soir!
Re,
En fait pour la 1) je crois que j'ai saisi...
en fait la fonction g de Tigweg est linéaire donc sa différentielle est elle meme et donc le rang de cette différentielle est la dimension de l'image de g,donc dg est de rang maximal d'ou g est une submersion et donc S(n,R) est une sous-variété de M(n,R).
Pour la dimension,ok mais on le sait que dim(S(n,R))=n(n+1)/2?
par contre pour le 2) faudrait que Camélia m'explique un peu plus
Salut robby3!
Ah, c'est donc ça, j'avais pas compris moi-même en fait!
Il faut que rg(dg)=dim(Im(g)) pour avoir une sous-variété?
ok mais on le sait que dim(S(n,R))=n(n+1)/2?
->Oui!Sinon c'est tout c... à voir, il suffit d'en exhiber une base!
Dès que tu places un 1 sur la partie strictement au-dessus de la diagonale, il faut aussi en placer un symétriquement puisqu'on est dans l'espace des matrices symétriques.
Dès que tu places un 1 sur la diagonale, tu obtiens une matrice symétrique sans rien faire de plus.
Tous les vecteurs (c'est-à-dire matrices!) obtenus ainsi forment une famille libre(petite vérification) et génératrice (il suffit de prendre une matrice symétrique et de la décomposer selon cette famille, mais on a tout fait pour!) donc c'est une base et il suffit de compter ses éléments!
Il y en a autant qu'il y a d'éléments au-dessus ou sur la diagonale, donc n (première ligne) +(n-1) (deuxième ligne)+...+1 (en bas) = n(n+1)/2.
La question 2 est claire robby3.
g est la composée d'une application bilinéaire et d'une applicaion linéaire, elle est donc indéfiniment différentiable.La différentielle en un couple (A,B) de l'application (A,B) -> AB est l'application linéaire qui àau couple de matrices (H,K) associe AK+HB (résultat classique)
donc la différentielle de g en M est l'application linéaire qui à H associe MtH+tMH-H.
Tu peux d'ailleurs aussi le vérifier directement.
Tigweg
salut Tigweg,
ok pour la 1er partie de ton post.
ok d'accord,c'est plus clair pour moi!
je vois je vois...
c'est quoi que Camélia appelle Dg_I ?
non mais en fait c'est bon,j'ai tout pigé!
Merci à tout les deux!!!
j'en poste tout de suite un qui y ressemble...
Désolé problème de connection!
Je rectifie une erreur à mon précédent post:
la différentielle de g en M est l'application linéaire qui à H associe MtH+tMH-Id (et pas -H!)
Avec plaisir
Il y a encore deux choses qui me turlupinent dans la solution de Camélia:
1)
et que si M est dans O(n,R), M est inversible
-> Cette précision sert-elle uniquement à prouver ensuite que Ker dg_M est isomorphe aux antisymétriques, ou a-t-elle une importance intrinsèque?
2)Est-il suffisant que dg_M soit de rang indépendant du choix de M pour conclure que {M,g(M)=0} est une sous-variété, ou bien est-il nécessaire que ce rang constant coïncide avec dim(g(E))?
Dans ce dernier cas en effet, on peut d'emblée affirmer que si {M,g(M)=0}est une sous-variété de E, alors sa dimension ne peut être que dim(E)-dim(g(E)).
Question subsidiaire:
le fait de s'autoriser à écrire sans aucune vérification dim(g(E)) laisse supposer que pour tout espace vectoriel normé E et toute application différentiable g:E->F (autre evn), g(E) est une sous-variété de F.
Cela est-il vrai?
Merci!
Tigweg
Est-il suffisant que dg_M soit de rang indépendant du choix de M pour conclure que {M,g(M)=0} est une sous-variété, ou bien est-il nécessaire que ce rang constant coïncide avec dim(g(E))?
>en fait quand tu as une application et que tu veux montrer que c'est une submersion(toujours dans le but de montrer qu'une chose est une sous-variété) il faut que Dg soit surjective cad de rang maximal égal à la dimension de l'espace d'arrivée
pourquoi c'est pas -H ?
c'est bien la différnetielle en H:
cad Dg(M).H non?
->Attends, on dit des bêtises tous les deux!
L'application M->I est constante donc sa différentielle est nulle!
Ainsi la différentielle de g en M est l'application linéaire qui à H associe MtH+tMH tout court, désolé!
en fait quand tu as une application et que tu veux montrer que c'est une submersion(toujours dans le but de montrer qu'une chose est une sous-variété) il faut que Dg soit surjective cad de rang maximal égal à la dimension de l'espace d'arrivée
->Ok, mais si g n'est pas linéaire, g(E) n'est pas un sev de l'espace d'arrivée F, donc quel sens donner à dim(g(E))?
Cela rejoint sans doute d'ailleurs ma
Question subsidiaire:
le fait de s'autoriser à écrire sans aucune vérification dim(g(E)) laisse supposer que pour tout espace vectoriel normé E et toute application différentiable g:E->F (autre evn), g(E) est une sous-variété de F.
Cela est-il vrai?
Waouh, ça à l'air 'achement intéressant tout ça. On en fait à partir de quand tout ça? (Il y a des prérequis ou on peut ça en commencer en live ? ).
salut toi!
si tu sais ce que c'est un difféomorphisme(je me damnde pourquoi je te pose la question!
bien sur que tu sais!
je pense que tu peux commencer ça quand tu le souhaite.
Eh non, on peut pas tout savoir.
Je vais essayer de voir ça quand j'aurai un temps, tes posts me seront précieux: poste un max dans ce cas!
ça par contre,je sais pas trop...je prefere m'abstenir,je risque de dire n'importe quoi!
->Ok!On attendra donc que Camélia, Kaiser, perroquet, raymond, lolo, blang , elhor ou autres K-Silver veuillent bien répondre!
Mais oui, me voilà. Je n'ai pas tout lu, mais je vais essayer de mieux expliquer.
1) Prenez-le comme vous voulez, les matrices symétriques forment un sous-espace vectoriel de dimension n(n+1)/2 (il suffit de connaitre les 1+2+...n coefficients du triangle supérieur) donc c'est une C
sous-variété de dimension n(n+1)/2.
2) GL_n(R)=det^{-1}(R*) est un ouvert de Mn(R) qui lui est un espace vectoriel de dimension n2. Soit g:GLnS(n,R) définie par g(M)=M tM-Id. D'abord c'est vrai que ça va dans S(n,R). Ensuite c'est vrai que O(n,R)=g^{-1}(0) (c'est ici que servait ma remarque du fait qu'une matrice orthogonale est inversible).
Soit définie par
(M)=(M,tM) Elle est linéaire, donc C et sa différentielle en chaque point est elle même.
Soit 
: (Mn(R))2Mn(R) définie par (A,B)=AB. Elle est bilinéaire, donc C et on a
D(A,B)(H,K)=AK+HB
Il se trouve que g est la restriction à GL(n,R) de o . Donc g est C et en écrivant comme d'hab la composition des différentielles on arrive à
DgM(H)=M tH+H tM
Pour pouvoir appliquer le théorème de submersion, il reste à voir que pour tout M dans O(n,R) DgM est de rang maximal. Pour ce faire, j'ai calculé la dimension du noyau.
Au point I Il est clair que Ker DgI est l'ensemble des matrices antysymétriques qui est de dimension n(n-1)/2 (il suffit de connaitre les termes au-dessus de la diagonale). Donc rg(DgI)=n2-n(n-1)/2=n(n+1)/2=dim S(n,R) et la question est reglée au point I.
Soit H dans Ker(DgM) pour M dans O(n,R). Alors
H M-1=H tM=-M tH=-t(HM-1)
ce qui montre que la multiplication à droite par M établit un isomorphisme entre Ker(DgM) et les matrices antisymétriques. Donc le calcul sur les dimensions, est le même et g est bien une submersion en chaque point de O(n,R).
3) O(n,R) est une sous-variété de dimension n(n-1)/2.
Merci mais pour ma part j'ai parfaitement compris tout cela.
Les 2-3 questions qui me turlupinent encore sont indépendantes de cet exercice particulier et sont exposées dans mon message de 12h27:
l y a encore deux choses qui me turlupinent dans la solution de Camélia:
1)
et que si M est dans O(n,R), M est inversible
-> Cette précision sert-elle uniquement à prouver ensuite que Ker dg_M est isomorphe aux antisymétriques, ou a-t-elle une importance intrinsèque?
2)Est-il suffisant que dg_M soit de rang indépendant du choix de M pour conclure que {M,g(M)=0} est une sous-variété, ou bien est-il nécessaire que ce rang constant coïncide avec dim(g(E))?
Dans ce dernier cas en effet, on peut d'emblée affirmer que si {M,g(M)=0}est une sous-variété de E, alors sa dimension ne peut être que dim(E)-dim(g(E)).
Question subsidiaire:
le fait de s'autoriser à écrire sans aucune vérification dim(g(E)) laisse supposer que pour tout espace vectoriel normé E et toute application différentiable g:E->F (autre evn), g(E) est une sous-variété de F.
Cela est-il vrai?
Merci!
Tigweg
Mais oui, me voilà
:D:D
Soit H dans Ker(DgM) pour M dans O(n,R). Alors
H M-1=H tM=-M tH=-t(HM-1)
ce qui montre que la multiplication à droite par M établit un isomorphisme entre Ker(DgM) et les matrices antisymétriques.
>ça je comprend pas.
M^{-1}=^tM non?
pourquoi
Salut Tigweg
J'avais besoin de savoir que O(n,R)
Gl(n,R) d'abord pour dire que O(n,R)=g-1(0), (comme ça g est défini sur un ouvert) et je m'en suis aussi servie pour dire que la multiplication par M établit un isomorphisme entre un Ker quelconque et les antisymétriques.
Maintenant pour les théorèmes:
Théorème de submersion: Soient U un ouvert de Rn, et F:U
Rm une fonction au moins C1. Soit y dans Rm et soit V=F-1(y).
Si V est non vide et si DFx est de rang m en chaque point x de V, alors V est une sous-variété de dimension n-m de Rn.
Théorème du rang constant: Même données.
Si V est non vide et si DFx est de rang k pour tout x d'un ouvert contenant V alors V est une sous-variété de dimension n-k de Rn.
Et tant que j'y suis:
Théorème d'immersion. Mêmes données.
On suppose que F est de rang n en chaque point de U et que F établit un homéomorphisme entre U et F(U). Alors F(U) est une sous-variété de dimension n de Rm.
D'accord Camélia, merci beaucoup pour ces précisions très claires.
Par contre pour le théorème d'immersion, ce n'est pas plutôt dF_U qui doit être de rang n en tout U?
(F n'est pas forcément linéaire, ou alors rg(F) a un sens plus général que je ne connais pas).
Du coup si F est une application de tout
dans
on ne peut en général pas affirmer que
est une sous-variété de
?
(ce qui était plus ou moins ma question subsidiaire).
Oui, tu as raison, je voulais parler de DF_x mais quand on fait de la géométrie différentielle c'est vite fait de faire l'abus de langage...
la réponse à ta question: NON. Il y a une hypothèse de plus.
Pour un contrexemple:
f:RR2 définie par
Elle est injective, Dft est toujours de rang 1, mais f(R) n'est pas une sous-variété de R2. Je fais le dessin sur demande...
Merci, mais j'avoue que je ne saisis plus très bien:
1)En quoi l'injectivité est-elle importante?
2)Comme Df_t est de rang constant, f(R) devrait être une sous-variété en vertu du théorème du rang constant, non?
Non, le thèorème du rang constant parle d'image réciproque. Ici, il est question d'image directe... L'hypothèse du théorème d'immersion parle d'homéomorphisme entre l'ouvert de départ et l'image. Le fait que f soit injective assure que f est une bijection continue sur l'image. Et pourtant, ça ne suffit pas...
Je suis désolé, ma connection à internet est très aléatoire aujourd'hui!
Il se peut que je sois coupé à nouveau, qu'on me pardonne donc si je ne réponds pas immédiatement.
Le fait que f soit injective assure que f est une bijection continue sur l'image. Et pourtant, ça ne suffit pas...
->D'accord!
Non, le thèorème du rang constant parle d'image réciproque.
->Oui en effet, suis-je bête...
f(R) n'est pas une sous-variété de R2
->Pour prouver cela, suffit-il de vérifier qu'il n'existe aucun entier m et aucune application g de classe C1 de R² dans Rm telle que g(f(R))=0 et telle que le rang de dg_(x,y) soit constant en tout point (x,y) de f(R)?
Ou cela n'est-il toujours pas suffisant?
Ou y a-t-il beaucoup plus élémentaire?
Oui, il y a plus élémentaire. Il suffit de la dessiner pour comprendre ce qui cloche...
Pour prouver cela, suffit-il de vérifier qu'il n'existe aucun entier m et aucune application g de classe C1 de R² dans Rm telle que g(f(R))=0 et telle que le rang de dg_(x,y) soit constant en tout point (x,y) de f(R)?
Même si tu prouvais celà elle pourrait encore être une sous-variété...
Ah oui?!
C'est exigeant, d'être une sous-variété, dis-moi!
Je veux bien la dessiner, mais comme je ne connais pas la définition des sous-variétés, je ne pense pas que je serai en mesure de repérer ce qui cloche!
Oui, c'est exigeant. Mettons, en gros, qu'une sous-variété de dimension k est un ensemble X tel que autour de chaque point il y a une boule telle que l'intersection de cette boule avec X est homéomorphe à un ouvert d'un espace vectoriel de dimension k.
Une sous-variété de dimension 1 est un truc qui localement ressemble à un bout de droite.
D'accord, je commence à saisir l'intuition du truc!
Donc dans notre exemple, il suffirait de se convaincre que tout voisinage d'un point de notre courbe contient quelque chose qui ressemble plus à une portion de plan qu'à une portion de droite?
Voilà la chose... Tous les voisinages de (0,0) contiennent un machin qui ressemble à une croix, mais certainement pas à un segment de droite...
Annuler
connectez vous
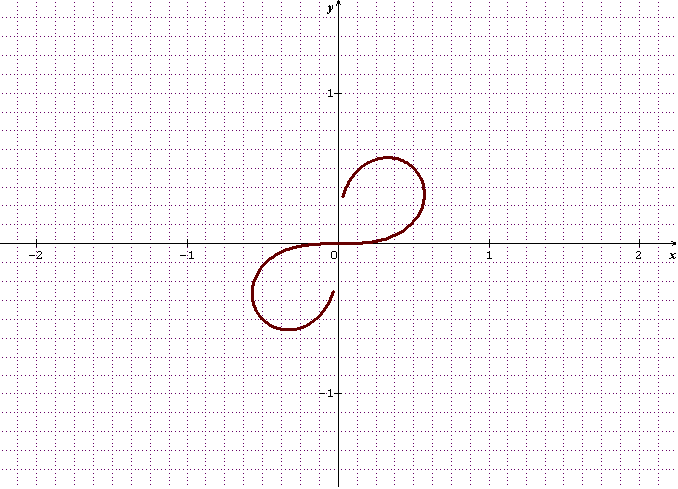
géométrie en post-bac