Inscription / Connexion Nouveau Sujet
Géométrie et fonctions polynômes
Bonjour à tous !
Avant de vous poser mon problème, je vais déjà vous faire part de mon énoncé :
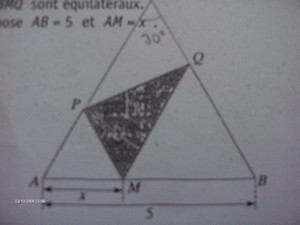
« On considère un point M sur [AB]. Les triangles AMP et BMQ sont équilatéraux. On pose AB=5cm et AM=x
Questions : « 1) Montrer que l'aire d'un triangle équilatéral de côtés de longueur a s'écrit : (a² 3)/4 »
3)/4 »
J'ai déjà fais cette question, j'ai posé la propriété de Pythagore pour avoir la hauteur :
a² = (1/2a)² + h²
h²= a²-1/4a²
h²=3/4a² h= 3/4
3/4
J'ai posé la formule : Atriangle = (Base*h)/2 =(a²*(1/2)* trois)/2=…=( a²
trois)/2=…=( a² trois)/2
trois)/2
2) « Déterminer la position de M pour laquelle l'aire de PQM est maximale. »
Et…c'est là que ça se complique : j'ai juste trouvé des égalités :
AM=AP=PM=x
AB=5
MB=MQ=5-x
Aussi par la propriété de Thalès j'ai démontré que si APM et MQB sont équilatéraux : (AP) et (MQ) sont parallèles, mais je vois pas à quoi conclure…
Merci de me donner des petites astuces 
Bonjour,
ABC est aussi équilatéral puisqu'il possède deux angles de 60° (en A et en B).
De plus, en utilisant le théorème de Thalès, tu peux montrer que AM = CQ et MB = PC. Donc, finalement, MPQ et PQC sont isométriques, donc ils ont la même aire.
Comme ABC, APM et MBQ sont équilatéraux, la question 1) te permet d'exprimer leurs aires.
Et auras donc à résoudre l'équation:
Aire(ABC) = Aire(AMP) + Aire(MBQ) + 2*Aire(PMQ).
D'où l'expression de l'aire de PMQ en fonction du reste.
Cela te donne une fonction en x qu'il te faut étudier pour en extraire son maximum...
Voilà une démarche possible,
padawan.
bonjour
Pour la première question
j'ai trouvé h= (3/4)a² soit a
(3/4)a² soit a (3/4)
(3/4)
Aire du triangle = (B*H)/2
ou
a*a/2 3/4=a²/2
3/4=a²/2 (3/4)=(a²/4)
(3/4)=(a²/4) 3
3
On peut aussi démontrer que les triangles PQM et PQC sont respectivement rectangles en P et en Q
donc aire de PQM = PM.PQ/2
or PM = x et PQ2= PC2 - CQ2= (5-x)2 - x2 = 25 - 10x
donc PQ =  (25-10x)
(25-10x)
donc aire de PQM = x (25-10x) / 2
(25-10x) / 2
Merci à tous pour vos réponses, j'ai pris la solution de Padawan, simplement je rencontre un autre problème :
j'ai donc posé : Aire(ABC) = Aire(AMP) + Aire(MBQ) + 2*Aire(PMQ), j'en arrive à :
(5² 3)/4 = (x²
3)/4 = (x² 3)/4 + ((5-x)²
3)/4 + ((5-x)² 3)/4 + 2* (PQ*PM)/2
3)/4 + 2* (PQ*PM)/2
ce qui me donne : (25 3)/4-(x²
3)/4-(x² 3)4-((5-20x+x²)
3)4-((5-20x+x²) 3)/4 = PQ*x
3)/4 = PQ*x
ensuite je met tout du même coté pour avoir une solution égale à zero :
(25 3-x²
3-x² 3-5
3-5 3 +20x
3 +20x 3 -x²
3 -x² 3)/4 -(PQ*x)=0
3)/4 -(PQ*x)=0
pour terminer à (-2x² 3 +20x
3 +20x 3 +20
3 +20 3)/4 -PQ*x = 0
3)/4 -PQ*x = 0
Mais je n'arrive pas à terminer sur une fonction polynome, car je suppose que c'est à ça que je dois arriver pour poser : -b/2a pour avoir la valeur maximale (sommet de l'équation)
A non mais en fait j'ai faux 
je viens d'essayer par une autre méthode, par celle de Th29 :
déjà je démontre que PCQM est un parallélogramme , donc les triangle PQM et PCQ sont rectangle en P et en Q, je calcule PQ comme Th29 l'a fait,ensuite l'aire de ces triangles : 2(B*h)/2 = x 25-10x)
25-10x)
Ensuite je reprends la formule Aire(ABC) = Aire(AMP) + Aire(MBQ) + 2*Aire(PMQ)
donc 0 = Aire(AMP) + Aire(MBQ) + 2*Aire(PMQ) - Aire(ABC)
= (x² 3 + (5-x)²
3 + (5-x)² 3 +4x
3 +4x 25-10x -25
25-10x -25 3)/4
3)/4
=(2x² 3 -10x
3 -10x 3 -20
3 -20 3 +4x
3 +4x 25-10x)/4
25-10x)/4
Mais il y a toujours ce 4x 25-10x qui m'empêche d'avoir une équation de degrés deux!
25-10x qui m'empêche d'avoir une équation de degrés deux!
Oh j'avance toujours pas pour cet exercice, j'ai juste vue que ce que j'avais pouvais ce simplifier pas 2, en donnant ainsi x² 3-5x
3-5x 3-10
3-10 3+2x
3+2x 25-10x) -2
25-10x) -2
Svp aidez moi 
Bonjour à tous!
j'ai moi aussi un problème à soumettre.
f'ai le même sujet mais ma question est:
On cherche à déterminer la position de M pour laquelle l'Aire du triangle MPQ est maximale ainsi que la valeur de cette aire.
Quelqu'un pourrait-il maider??!!
Merci.
Salut Tin !
Alors bin moi je peux t'aider car j'ai eu la même question  :
:
Il faut que M soit au milieu de [AB] Car si tu lis normalement ce que j'avais posté au-dessus on doit avoir à un moment donné : Aire PQM = (Aire ABC -(Aire APM +Aire MQB))/2
d'où à la fin : (-x² 3 +5x
3 +5x 3)/ 4 on a ainsi un polynome de degré 2 avec le sommet = -b/2a tu vas trouver si ton calcul est bon :S= 5/2=2.5 soit milieu de [AB]
3)/ 4 on a ainsi un polynome de degré 2 avec le sommet = -b/2a tu vas trouver si ton calcul est bon :S= 5/2=2.5 soit milieu de [AB]
Voili, si t'as un autre pblm... tu le dis 



