Inscription / Connexion Nouveau Sujet
dm de mathématique terminal S
bonjours a tous , j'espere que vous avez passé un bon reiveillon de noël ,voila j'ai un dm se mathématique que j'ai presque fini , mais il ya une question qui me pose problème
voici l'énoncé :
Dans le plan complexe rapporté au repère orthonormal direct , unité graphique : 4 cm, on considère les points A, B et C d'affixes respectives a, b et c telles que :
a = 1 - i, b = 1 + i c = -1 + i = -a.
On note G le cercle de diamètre [AB].
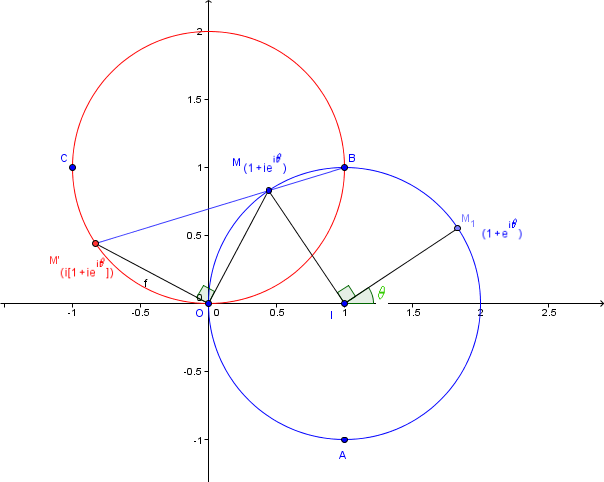
1°) a) Placer sur une figure les points A, B, C et le cercle G .
b) Mettre les nombres complexes a, b et c sous forme trigonométrique.
c) Soit r la rotation de centre O telle que r(A) = B.
Déterminer l'angle de r et le point r(B), image de B par r.
d) Déterminer l'image G ' du cercle G par r ; placer G ' sur la figure.
2°) On considère un nombre 
 ]o;2
]o;2 [ distinct de
[ distinct de  ; on note M le point d'affixe z = 1 + ie^i
; on note M le point d'affixe z = 1 + ie^i .
.
On désigne par M' l'image de M par r, et on appelle z' l'affixe de M'.
a) Montrer que M est un point de G distinct de A et de B.
b) Exprimer z' en fonction de z.
Calculer en fonction de  les affixes u et u' des vecteurs et BM et BM'
les affixes u et u' des vecteurs et BM et BM'
c) Etablir la relation : u = u' tan( /2) .[i][/i]
/2) .[i][/i]
d) Prouver que les points B, M et M' sont alignés.
Placer sur la figure un point M et son transformé M'.
je sais que l'angle de rotaion vaut  /2. j'ai tout réussi sauf la question c partie 2 est ce que quelqu'un aurait une idée merci d'avance
/2. j'ai tout réussi sauf la question c partie 2 est ce que quelqu'un aurait une idée merci d'avance 
j'ai encore un exercice et la je coince sur la dernier question :
je sais que f(x) = x admet une solution unique sur ]0;1[
sur ]0;1[
de plus je sais que f(x) est décroissante sur cette intervalle et que f(x) =f(1/x) quand x>0
je sais aussi que f(x) = 1/x admet une solution unique  sur l'intervalle ]1;+
sur l'intervalle ]1;+ [
[
de plus je sais aussi que f(x) est croissante sur cette intervalle
f(x) = 0.25x^2+1/4x^2-(lnx)^2
voila c'est tout ce que j'ai eu a démonter depuis le début de cette exercice pour en arrivé a cette question
merci d'avance 
bo509
En principe, nouvel exercice --> nouveau topic; mais comme c' est Noël...
Tu sais beaucoup de choses mais...
voila c'est tout ce que j'ai eu a démonter depuis le début de cette exercice pour en arrivé a cette question
... quelle question ?

ah oui désolé (je ne savais pas qu'il fallait un nouveau topic pour un nouvelle exercice j'en tiendrai compte la prochaine fois )
il faut donc prouvé que  *
* =1
=1
merci beaucoup pour ton aide
Je crois que quelque chose ne va pas dans ton écriture de :
Mets des parenthèses là où elles sont nécessaires:
Par exemple pour
écrire: f(x)=0.25x^2+1/(4x^2)-[ln(x)]^2

Non, je viens de vérifier;
Il existe bien tel que
et tel que
En valeurs approchées: et
Donc ça ne colle pas...




 distinct de A et B.
distinct de A et B.


