Inscription / Connexion Nouveau Sujet
Montrer qu'une suite est décroissante
Bonjour,
Je dois réviser pour un DS et j'ai un problème pour montrer qu'une suite est décroissante et minorée par 0.
Voici la suite
U0 = 1/2
Un+1 = (Un)^2 + 3/16
J'ai essayé Un+1 - Un mais ça ne me mène nulle part. Idem pour (Un+1)/Un
Pire, en posant Un+1 = f(Un) = (Un)^2 + 3/16
j'ai f'(x) = 2*Un
Et l'étude de signe montre que sur [0 ; +infini[ f(Un) est croissante !!
J'ai bien vérifié sur ma calculette, la suite est décroissante.
Quelqu'un a une idée svp ?
et d'ailleurs, j'ai oublié de demander, pourquoi le raisonnement que j'ai fait avec f(x) est faux ? Ca marche bien pour d'autres exos d'habitude...
(Désolé pour le double post, j'ai pas trouvé de fonction éditer)
Allons y 
c'est vrai pour
vu que
.
supposons
alors
et donc
c'est à dire
récurrence terminée avec succés

pour tout
on a
notre suite est donc bien décroissante et comme elle est minorée (par par exemple)
elle converge vers un réel et vérifiant
...
 sauf erreur bien entendu
sauf erreur bien entendu
Désolé encore une fois du double post, mais pourquoi la méthode avec f(x) ne marche-t-elle pas ici ?
Si elle marche ! Il fallait tout simplement ( après avoir prouvé la croissance de sur
)
justifier que tous les sont dans
puis comparer et
pour pouvoir déterminer la monotonie de la suite
et comme on a
...
et une petite récurrence donne pour tout
 sauf erreur bien entendu
sauf erreur bien entendu
Euh je ne comprends pas vraiment
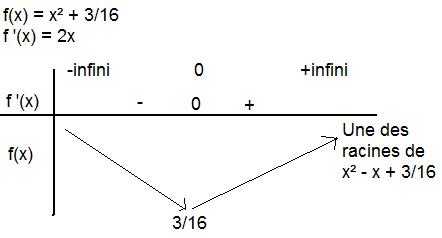
Voila le tableau de signe que j'obtiens (image attachée)
J'ai qui est croissante sur [0 ; +infini[ alors que je dois montrer qu'elle est décroissante
Par contre je comprends bien que tous mes sont sur [0 ; +infini[
up svp, je ne comprends toujours pas comment une suite peut être décroissante alors que la fonction est croissante
Bonjour
Tout simplement, Il se trouve que
, ce qui n'a rien de contradictoire! A partir de là, la croissance de f impose
...
ah d'accord, je comprends mieux merci 
Donc en fait cette méthode (de l'étude de signe par la fonction) n'est pas très utiles, puisqu'il faut quand même faire une récurrence après.
Mieux vaut faire la méthode de elhor_abdelali
En fait elhor (que je salue  ) utilise aussi la croissance de f qu'il redémontre implicitement. Ce qu'il faut retenir, c'est que si f est croissante, le sens de variation de la suite ne dépendra que de la position de
) utilise aussi la croissance de f qu'il redémontre implicitement. Ce qu'il faut retenir, c'est que si f est croissante, le sens de variation de la suite ne dépendra que de la position de par rapport à
D'accord, donc comme c'est vachement plus simple sans récurrence je vais étudier les signes alors^^
Merci pour votre aide



 analyse en post-bac
analyse en post-bac