Inscription / Connexion Nouveau Sujet
construire un quadrilatère
Bonsoir tout le monde
Mon problème c’est de construire un quadrilatère EFGH quelconque
Connaissant que les milieux de ses cotes forment un parallélogramme ABCD
et merci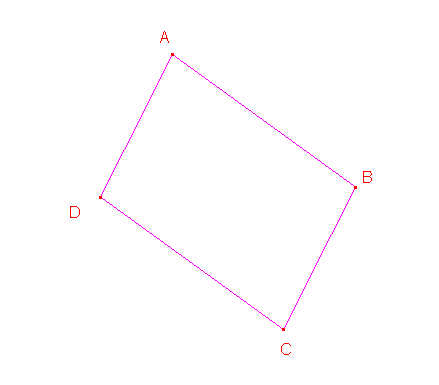
édit Océane : merci de poser tes questions sur le forum adéquat 
Démontre que les milieux des quatre côtés d'un quadrilatère quelconque déterminent un parallélogramme !
Cela signifie que si l'on appelle MNPQ les sommets du quadrilatère que tu cherches, avec
A milieu de MN
B milieu de NP
C milieu de PQ
D milieu de QN
Alors, tu peux choisir M, par exemple absolument n'importe où, puis tracer N symétrique de M par rapport à A, puis P symétrique de N par rapport à B, etc... 

Merci Pythamede de votre réponse
Mais le problème ce que la dernière symétrie ne coïncide pas avec le point A
C'est très difficile a réalisé
la dernière symétrie ne coïncide pas avec le point M point du depart
Ben il faut le faire avec soin... Ca devrait marcher, sinon...
Est-ce que l'on t'a donné le parallélogramme ABCD ?
Si oui, quelles sont les coordonnées des 4 points ?
Si non, tu peux tricher : Tu traces d'abord MNPQ quelconque, puis tu prends les milieux ABCD !
bonjour pythamede
ils on donné le problème comme défi sans coordonnées
et ils demande la méthode de construction
merci
Dans ce cas, définis toi-même les coordonnées de A,B,C et D.
A(0;0)
B(1;3)
C(6;4)
D(5;1)
par exemple.
Ensuite, tu choisis au hasard les coordonnées de M. M(1;-1)
les coordonnées de N sont alors (-1;1)
les coordonnées de P sont alors (3;5)
les coordonnées de Q sont alors (9;3)
les coordonnées du symétrique de Q par rapport à D sont alors (1;-1), c'est à dire celles de M !
Il faut bien sûr choisir au départ un point M extérieur au parallélogramme, d'une part, et tel que la droite AM ne coupe le parallélogramme qu'en A, d'autre part ! Je pense que la construction marcherait quand même, mais le quadrilatère formé si l'on ne prenait pas ces précautions serait probablement non convexe !
pythamede merci
mon problème c'est que les coordonnées ne sont pas données en plus le problème est dans un chapitre de translation je voit pas la relation
Merci a toi pour vos aides
Je sais ! C'est pour cela que je te propose de dessiner selon ces coordonnées ! Puisqu'elles ne te sont pas imposées ! Avoir des coordonnées précises te permettra de tracer correctement tous les points, même si tu traces par ailleurs les "constructions" que l'on te demande !
Tout cela n'est qu'une aide pour que tu puisses dessiner correctement ! Cela parce que tu ne sais pas faire un dessin suffisamment précis pour que ça marche !
Bonjour
Je croire que a chaque parallélogramme est associer un quadrilatère unique
Donc le chois au hasard de M ca marche pas
Et moi je dis que ça marche très bien. En prenant le parallélogramme que tu as fourni ci-dessus, la figure ci-jointe te montre trois quadrilatères différents dont les milieux des côtés sont bel et bien les quatre sommets de ton parallélogramme ABCD !
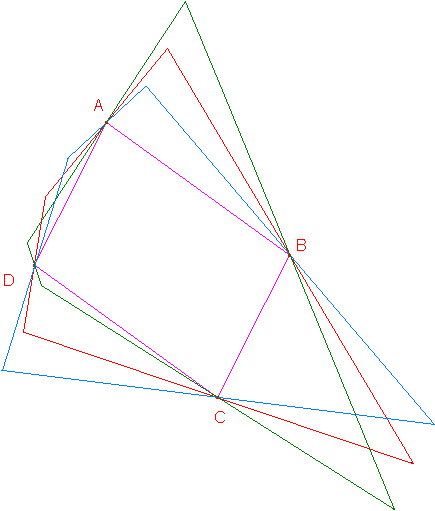
oui pythamede merci infiniment
maintenant j'ai compris
La composée de deux symétries de centres A et B c'est la translation de vecteur 2vecteur AB
et comme ABCD est un parallelogramme on a La composée
SA o SB o SC o SD de M = M
merci
N'oublie pas ce que je t'ai dit hier à 12h59 :
Démontre que les milieux des quatre côtés d'un quadrilatère quelconque déterminent un parallélogramme !


