Inscription / Connexion Nouveau Sujet
Dm suites à récurrence et somme de termes...
Bonsoir tout le monde!
Voila, après y avoir passée toute cette après-midi à chercher la solution, je me résigne à poster ici...
EXO 1:
On considère le suite (Un) définie par :
Uo = 3
U(n+1) = 2/(1+Un)
1) Démontrer que, pour tout n
 , on a 0
, on a 0 Un
Un 3
3
aucune idée de comment faire???
2) On considère la suite Vn définie, pour tout n
 , par : Vn = (Un-1)/(Un+2)
, par : Vn = (Un-1)/(Un+2)
Démontrer que Vn est géométrique.
Alors, j'ai bien essayé de trouver q via U(n+1)/Un, après avoir trouvé que U(n+1) = (1+Un)/(4+2Un), mais au final de ce quotient, je me retrouve avec ce résultat (Un²-1²)/(2Un²+4Un+12) et je sais pas du tout quoi en faire...
3) Exprimer Vn en fonction de n. En déduire la limite de la suite Vn
ça à mon avis il doit falloir que je trouve q auparavant et que je mette sous la forme mais sans la question 2, cela me semble impossible.... quand à la limite je ne me souviens plus comment faire mais avec la forme Un= .... je dois pouvoir retrouver ça dans mes cours...
4)En déduire la limite de Un.
Je pense que j'ai besoin des questions précédentes pour ça...
EXO 2:
Soit n
 -(0)
-(0)
On désigne par Sn la somme des cubes des n premiers entiers naturels impairs:
Par exemple,
1) Démontrer par récurrence que pour tout n
 , Sn = 2n^4-n²
, Sn = 2n^4-n²
HOURRA, une question ou j'ai trouvé la réponse! (bon j'avoue, grâce à une vidéo sur dayli expliquant la méthode par récurrence... mais quand même x) )
2) Déterminer n tel que :
Et après en lisant cette question j'ai déchanté.... ^^ j'ai essayé en resolvant un peu au pif l'équation 2^4-n² = 913276, mais vous vous doutez que je n'ai rien trouvé de concluant....
Voila, merci de me laisser juste des pistes s'il-vous-plait, j'aimerais réfléchir un maximum par moi-même, ça me tient à coeur de comprendre ce dm( qui est déjà le deuxième de l'année grrrr) ^^
Bonsoir,
En principe, un exercie par topic; je réponds au premier:
1) Soit la fonction définie par
sur
et
est décroissante sur
Ainsi
soit
Donc
On est maintenant en mesure de faire une récurrence sur la propriété :
Pour tout
Initialisation:
et
est vraie.
Hérédité:
On suppose que est vraie pour un certain rang
fixé.
donc , et
et l' hérédité est prouvée.
C' est un début...

Bonjour, désolé de ma longue absence, mais j'étais très occupé avec mes autres devoirs...
j'ai plusieurs questions en ce qui concernent ta réponse(merci d'avoir tout résolu, je n'en demandais pas tant!  ) :
) :
-pour la question une, pas de problème, j'ai compris le raisonnement, si ce n'est que je me demande si on est obligé de poser U(n+1)= f(x),en effet on est en mesure de dire que comme cet encadrement est valable pour U(n+1), alors il est valable pour Un, étant donné que Un+1 est décroissante non?
-pour la question 2, j ne comprend pas tes calculs à partir de jusqu'à la fin, je ne vois pas les opérations que tu effectues pour trouver ces résultats...
-pour la question 3 je vois l'idée, mais je ne comprend pas comment tu passes de à
-et pour la question 4 en revanche, je ne comprend pas le raisonnement...
Merci de prendre la patience de m'expliquer tout ça! =) (si je n'ai pas fait de topic pour l'exo deux, c'est d'une, parce-que je ne savais pas pour cette règle, et de deux, parce-que créer un topic pour une seule question d'exercice me semble un peu abusé peut-être?)
Re,
Il va falloir apprendre à calculer damouf 
1) Ta suite est une suite définie par récurrence avec
avec
C' est une règle générale: pour ce type de suites, il est pratique d' étudier les variations de .
Cela à permis de prouver que si ;, alors
Ensuite, l' hérédité de la récurrence tombe toute seule.
2)
3)
Tu as oublié le signe "-"
4) On a en fonction de
avec:
On cherche à exprimer en fonction de
:
Donc
et car
et

re,
C'est vrai que j'ai quelques soucis pour calculer, mais c'est surtout en général que j'arrive pas à sortir des factorisation du chapeau ou à bidouiller des fractions aussi aisement qu'il ne le faudrait ^^
Bon ça mis à part, j'ai à peu près tout compris, sauf encore à la question 2, où jai beau poser le calcul en tous sens, je ne comprend pas cette ligne la, sans doute quelque chose de simplissime qui m'échappe, mais en tout cas ça m'échappe x)
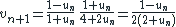
oui, cette partie la, j'avais vu la factorisation, la ou je comprend pas c'est la première partie ou l'on multiplie par
oui, d'accord, mais quand j'effectue ce produit, je trouve après avoir factorisé par Un... (je crois que j'avais mal compris ta réponse précédente en fait)
ha ouiiiiiii ça y est j'ai vu le truc! effectivement la bête règle du produit en crois ^^' merci de ta patience!!! =D


