Inscription / Connexion Nouveau Sujet
Produit de convolution
Bonjour à tous,
J'ai de nouuveau fort à faire avec un exercice de traitement de signal à propos du produit de convolution.
En fait, c'est un signal carré valant 1/T entre -T/2 et T/2 --> pour simplifier, le signal est nul ailleurs.
On me demande de prouver que x(t)*x(t) = y(t)
x(t) est le signal en question(defini comme suit : x(t) = 1/T Rt(t)), y(t) est un signal triangulaire existant entre -T et T et valant au plus 1/T.
j'ai donc tout d'abord décalé mon x(t) en x(T/2 - t)
x(t)*x(t) = int de -T/2 à T/2 de (1/T x Rt(t) x 1/T x Rt(T/2-t)) dt
Mais là je trouve '1' !
J'ai ensuite essayé en partant du principe que x(t)*x(t) = X(f).X(f)
Mais je galère aussi :
X(f) = int (1/T Rt(t).exp(2PIjft)dt) or vu que le signal n'existe qu'entre -t/2 et t/2, les bornes se changent en -t/2 et t/2
ça donne donc:
X(f) = 1/T int de -t/2 à t/2 ((1/T).exp(2PIjft)dt)
et je trouve exp(PIj)-exp(-PIj).(-1/2PIjf) = 0
Quelque'un peut m'aider à trouver mon erreur ?
Bonjour,
Ton erreur vient de la définition de la convolution et d'un mélange des lettres 
on a pour la convolution:
Normalement, en intégrant, tu auras une fonction de t.
Je te laisse continuer par toi même. N'hésites pas à revenir en cas de difficulté.
Ptitjean
merci de ta réponse mais le principal problème que j'ai tient dans ce 't' !
Je ne comprends pas ce que c'est.
Dans ton exemple, u est bien la variable de la fonction puisqu'on a un "du", mais qu'est-ce que ton "t" signifie ?
bonjour,
pour intégrer, tu considères t comme une constante
t, c'est la variable de ta fonction finale
on peut poser F(t) comme la convolution des deux fonctions x(t) et x(t)
par exemple, on peut définir une fonction comme:
ce qui donne
Ce qui peut déranger, c'est que d'habitude en mathématique, la variable est x et on parle de fonction f ou g.
en traitement du signal, il est courant de prendre t comme variable (t comme le temps) et x comme fonction pour la fonction échelon
ptitjean
En fait, il eut été souhaitable de définir le produit de convolution de f et de g par:
f*g: R->R tel que (f*g)(t)=intégrale(-oo..+oo)f(u)g(t-u) du sous des hypothèses raisonnables pour que tout ait un sens quoi mais voilà.

merci à tous pour ces réponses.
Si vous lisez mon premier post, vous verrez que c'est ce que j'ai fait :
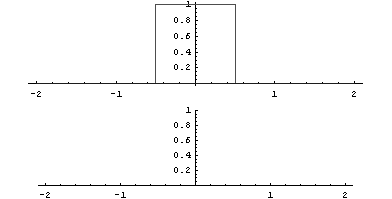
L'image attachée est le signal sur lequel je dois travailler.
Un signal entre -T/2 et T/2 qui convolutionner (??) à lui-même doit donner un signal triangulaire de période -T ; T
le signal est x(t)= 1/T x Rt(t)
1/T est, pour moi, une constante, donc peut être sortie de l'intégrale.
Et Rt(t) est égale à 1/T (amplitude su signal) entre -T/2 et T/2 : sur le reste de R c'est égal à 0.
Donc on arrive à :
r(t)*r(t) = intégrale(-T/2 à T/2)de (1/T Rt(t))x(1/T Rt(T/2 - t))dt
en décomposant on a donc :
si R*(t)= r(t)*r(t) on a :
R*(t)= 1/T² intégrale de -T/2 à +T/2 de Rt(t) x Rt(T/2-t)dt
En décomposant on a :
Soit
R1(t) = intégrale(-T/2 à T/2) de 1/T dt
donc
R1(t) = intégrale(-T/2 à T/2) de 1 dt = 1/T x (T/2 + T/2) = 1
Et c'est sur l'autre intégral que j'ai un problème : entre quelle bornes je dois l'intégrer ?
Il y a un décalage de T/2, donc je l'intègre de -T à 0 ou je reste sur -T/2 à T/2 ?
bonjour,
quite à me répéter, tu te trompes dans ton intégrale.
Reprends tes définitions de la convolution !!!
Je commence pour toi
Effectivement, Rt(u) est nul entre -T/2 et T/2 et vaut 1 autrement. On a donc
Maintenant, pour finir de calculer l'intégrale, je te suggère de différencier les cas.
Par exemple, que vaut Rt(t-u) pour u appartenant à [-T/2, T/2] si t<-T ?
Trouve les différents cas pertinents et calcule l'intégrale pour chaque cas.
Normalement tu devrais retomber sur ta fonction triangulaire.
Ptitjean
Petite erreur qui s'est glissée dans mon post précédent.
Rt(u) est bien sur nulle en dehors de l'intervalle [-T/2, T/2] et vaut 1 sur cet intervalle.
J'ai beau travaillé sur ce que tu m'as donné : je n'y comprends toujours rien.
En relisant à tête reposé ta réponse, j'ai compris qu'en fait le t que tu utilises (avec u comme variable) peut avoir n'importe quelle valeur dans le calcul.
Mais il deviendra la variable du resultat du pdt de convolution : c'est ça ?
Donc on a 2 valeurs intéressantes : T et -T.
si -T < t < 0 --> r(t-u) = r(-T-T/2) pour u = -T/2 donc r(T/2)= 1
Et si t = 0 on arrive à r(0-T/2)=r(-T/2)= 1 --> donc je dois intégrer r(t-u) = 1 entre -T/2 et T/2 et
j'aurai la fonction décrivant le pdt de convolution entre -T et 0 ?
Ensuite si 0 < t < T --> r(t-u) = r(0-T/2) = 1 et r(T-T/2) = 1 --> j'aurai la même fonction que dans le précédent cas !!!!
Je trouve ce sujet hyper compliqué et je n'arrive pas à lire qqchose de vraiment simple avec une vraie application claire du pdt de convolution : sans ça, je galère bcp !!!!
POuvez-vous m'aider (de nouveau ?)


 analyse en post-bac
analyse en post-bac