Inscription / Connexion Nouveau Sujet
Volume d'un cuboctaèdre
bonjour j'ai un dm de maths à faire mais je suis bloquée.
Pourriez-vous m'aider??
j'ai un cube de départ d'arête 8 cm puis en prenant les milieux et en reliant ces points ont obtient un cuboctaèdre qui mesure 4 2
2
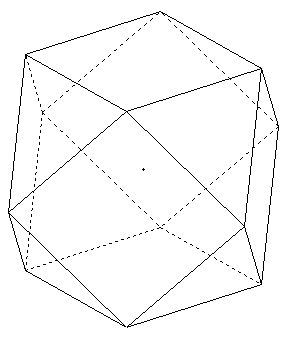
on peut observer que le cuboctaèdre peut être défini comme un cube auquel on aurait retiré en ses sommets le meme tétraèdre trirectangle.
La question est : Calculer le volume W du cuboctaèdre.
Je suis vraiment bloquée, j'ai cherché sous toute les formes et je ne vois a par en calculant le volume du cube qui est égal à 512 cm3 puis en calculant le volume d'un tétraèdre trirectangle (que je cherche) multiplié par 8 (8 tétraèdres) et les enlevés du volume du cube.
C'est a mon avis comme ça qu'il faut faire mais je n'arrive pas à calculer le volume d'un tétraèdre...
Aidez-moi s'il vous plait j'ai vraiment besoin de le réussir. 
Edit Coll : image placée sur le serveur de l'  Merci d'en faire autant la prochaine fois !
Merci d'en faire autant la prochaine fois ! 
![]() [lien]
[lien]
Dessine le cube et coupe la région de l'un de ses sommets, comme il est dit dans l'énoncé, pour faire
apparaître l'un des 8 tétraèdres.
Tu calculeras facilement son volume si tu prends pour base non pas sa face délimitée par un triangle
équilatéral, mais l'une de ses autres faces contenues dans les plans des faces du cube.
Bonsoir
Un tétraédre a pour base un triangle équilatéral de côté 4 2 et de hauteur 2
2 et de hauteur 2 6 dont l'aire A = 4
6 dont l'aire A = 4 2.2
2.2 6/2 = 8
6/2 = 8 3
3
et les 3 autres arètes ont pour longueur 4
La hauteur du tétraèdre est un côté de l'angle droit d'un triangle rectangle d'hypothénuse de longueur 4 et l'autre côté de l'angle droit a pour longueur 2.2 6/3 = 4
6/3 = 4 6/3 ( les 2/3 de la hauteur = les 2/3 de la médiane) =>
6/3 ( les 2/3 de la hauteur = les 2/3 de la médiane) =>
hauteur du tétraèdre =  (4²-16.6/9) = 4/
(4²-16.6/9) = 4/ 3
3
=>
Volume d'un tétraèdre = 8 3.4/
3.4/ 3/3 = 32/3
3/3 = 32/3
=>
W = 512 - 8.32/3 = 512-256/3 = (1536-256)/3 = 1280/3 ( 5. 2.(4
2.(4 2)3/3 voir google)
2)3/3 voir google)
A++
Re
En effet Priam
pour calculer le volume d'un tétraèdre il est bien péférable de prendre pour base le triangle rectangle de côtés de l'angle droit ( quel idiot je suis ; j'ai bêtement suivi l'idée de landes7640) 4 et 4 dont l'aire = 8 et la hauteur = 4 =>
=>
volume d'un tétraèdre = 8*4/3 = 32/4
A+
merci beaucoup pour votre réponse rapide!
Merci beaucoup à toi geo3 tu m'a vraiment bien aidée!
j'ai encore un peu de mal à comprendre comment tu as fais mais merci beaucoup !!!
juste une petite présision:
La hauteur du tétraèdre est un côté de l'angle droit d'un triangle rectangle d'hypothénuse de longueur 4 et l'autre côté de l'angle droit a pour longueur 2.26/3 = 46/3 ( les 2/3 de la hauteur = les 2/3 de la médiane) =>
hauteur du tétraèdre = (4²-16.6/9) = 4/3
je ne comprend pas cette partie ?? pourrais tu me la détaillé (si c'est possible)
merci encore !!
Si on prend comme base du tétraèdre l'une de ses faces en forme de triangle rectangle isocèle, les côtés de l'angle droit d'un tel triangle ont pour longueur 4. Son aire vaut donc 4x4/2,
La hauteur du tétraèdre par rapport à cette base est un côté semblable d'une autre de ces trois faces; elle a également pour longueur 4.
Le volume du tétraèdre est donc égal à 1/3*(4*4/2)*4 = 32/3.
une dernière question:
je comprend pas le volume W,
W = 512 - 8.32/3 = 512-256/3 = (1536-256)/3 = 1280/3
d'ou viens le (1536-256)?????
merci Priam pour ta réponse c'est comme cela que j'avais fait au début mais normalement un tétraèdre n'a-t-il pas comme base un triangle équilatéral ??
Pas forcément.
D'une manière générale, un tétraèdre est un solide à 4 faces planes, qui sont en forme de triangles.
Dans le cas présent, il s'agit d'un tétraèdre trirectangle.
Bonsoir
Suit la méthode de Priam c'est bien plus simple
sinon
1)un tétraèdre n'a pas nécessairement pour base un triangle équilatéral et si tu prends une autre face comme base de ce tétraèdre on a un triangle rectangle isocèle ( de côté 4) comme base et la hauteur de ce tétraèdre est 4 ( comme Priam a dit)
*
2)
Si on prend comme base de ce tétraèdre le triangle équilatéral de côté 4 2 : une hauteur de ce triangle a bien pour longueur 2
2 : une hauteur de ce triangle a bien pour longueur 2 6 et l'aire de ce triangle est bien 8
6 et l'aire de ce triangle est bien 8 3
3
*
3)
Si alors on projette le sommet sur la base (de ce triangle équilatéral) on obtient le centre de gravité du triangle équilatéral qui se trouve au 2/3 de la médiane ( qui aussi hauteur)
*
4)En prenant comme volume d'un tétraèdre = 32/3 ; 8 tétraèdres = 8.32/3 = 256/3
et
W = 512 - 256/3
A+
merci encore pour vos réponses !
mais je ne comprend pas si je fais 512-256/3 cela me fait 256/3
mais d'ou viens le 1536 ???
c'est juste le point ou je n'ais pas compris.
Re
Allons 512-256/3 signifie 512 - (256/3) = (1536 - 256)/3 en réduisant 512 au même dénominateur 3
et 1526 - 256 = 1280
tandis que toi tu as pris 512 - 256/3 pour (512 - 256)/3 qui n'est pas la même chose ; il faut faire attention aux parenthèses.
A+
ah d'accord merci beaucoup!
J'ai rendu mon devoir hier nous verrons bien le résultat !
Merci encore !


