Inscription / Connexion Nouveau Sujet
Déterminer une longueur
Bonjour,
j'ai un peu soucis, celui de ne rien comprendre à mon dm.
On considère un trapèze rectangle PQSR dont les dimensions sont données dans la figure en dessous. On cherche à savoir s'il existe un point M sur le segment [PQ] tel que l'angle SMR soit droit.
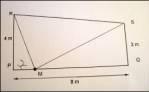
On note x la longueur du segment [PM].
1_Montrer que pour tout réel x,
x²-8x+12=(x-4)²-4
2_Mettre le problème en équation, puis résoudre l'équation obtenue.
3_Conclure.
Edit Coll : image placée sur le serveur de l'  Merci d'en faire autant la prochaine fois !
Merci d'en faire autant la prochaine fois ! 
![]()
Est-ce qu'on pourrait avoir la figure en plus grand car on n'arrive pas à lire les valeurs et les lettres..
Bonjour Chloé. Qu'est-ce que tu ne comprends pas ?...Tout
est expliqué, pourtant ... j'ai plutôt l'impression que tu ne sais pas comment faire , non ?.....
Pour montrer qu'il y a un angle droit en M, il faut prouver que le triangle RMS est rectangle en M ...
Et tu peux calculer ses côtés avec les autres triangles rectangles : triangle PRM pour déterminer le côté gauche RM, et le triangle rectangle MQS, pour le côté droit MS ...
Alors, vas-y !...
Pour la première question tu résoud le membre de droite et tu retombes sur le membre de gauche
(x-4)²-4= x²-8x+16-4
= x²-8x-12
jacqlouis non effectivement je ne vois pas comment faire.
Mais il manque des mesures. Faut calculer avec quoi ? Je ne vois pas
Célinou > merci.
Je recommence : calcule d'abord l'hypoténuse de RPM, avec ses côtés RP = 4 , et PM = x . Tu as tout ce qu'il faut pour appliquer Pythagore ...
Bon alors si j'ai bien compris ça me donne
RM²=RP²+PM²
soit RM²=16+x²
et pour le triangle SQM
SQ²+QM²=SM²
Soit 9+(PQ-PM)=SM²
Ce n'était pas vraiment difficile à comprendre , non ?
Que vaut PQ et que vaut PM : remplace-les donc par leur valeur ...
ah oui j'ai oublié de l'écrire.
QM²=9+(64-x²)
Oui je voyais vraiment pas si on pouvait utiliser Pythagore mais maintenant ça va merci.
Mais ce qui me pose le plus de problème c'est l'équation qu'il faut trouver.
Ce que tu viens de donner , c'est SM² ...
Donc , il te reste à comparer RM² + SM² à RS² .
Il faut que détermines ce RS² ...
Si tu traces une horizontale à partir de S, qui coupera RP en T , tu auras (nouveau triangle rectangle ! ), le moyen de calculer RS ² ... D'accord ?
Ah oui. Merci. Et ensuite une fois qu'on a trouvé ceci, comment fait-on avec l'histoire d'équation de l'énoncé ?
Finalement, tu as obtenu quoi pour montrer que le triangle RMS pouvait être rectangle ... Quelle équation ?..
On verra après, " l'histoire " dont tu parles ...
Désolé mais je ne vois vraiment pas.
On a l'hypoténuse du triangle RMS
RM²+MS²=RS²
9+64-x²+16+x²=64
C'est ça ?
Bonjour, Chloé . Hier, à 11h56, je t'ai dit ce qu'il fallait faire ...
Je recommence . Tu as calculé ( RM² + MS² ) en fonction de x ... OK...
Maintenant il faut calculer la vraie valeur de RS², avec les données chiffrées de l'énoncé .
Fais donc comme je t'ai dit : tu traces la droite ST (parallèle à QP), et tu as ce nouveau triangle rectangle, de cotés ST = 8, TR = 4-3 = 1, et d'hypoténuse SR ....que tu vas calculer avec ST et TR .
Que trouves-tu comme longueur pour SR (avec Pythagore, bien sûr). Dis-moi ce que tu trouves d'abord, et ...on pourra finir l'exercice après !...
Voilà, enfin, la bonne réponse ...presque ! car 65 , c'est RS² ...
Donc maintenant, nous pouvons écrire la condition nécessaire pour que le triangle MRS soit rectangle .
Il faut que l'on ait : RM² + MS² = RS²
Tu fais cela, et tu me dis ce que tu as obtenu ...
Je te rappelle : RM² = x² + 16
et : MS² = (8 - x )² + 9
RM²+MS²=RS²
x²+16+(8-x)²+9=65
x²+16+64-16x+x²+9=65
x²+x²-16x+89=65
Pour le moment c'est bon ?
Après ça me semble ne pas être ça, donc si je pars mal au début ...
Tu aurais pu mettre dans l'ordre (des puissances de x) , c'est mieux !
Et tu peux simplifier par 2, c'est plus smple ,... forcément !
Ce qui donne : x² - 8x + 12 = 0 ... Equation à résoudre .
Pour trouver la solution, tu vas faire apparaître le développement d'un carré :
(x² - 8x) est le début de (x² - 8x + 16) qui est (x - 4)²
Tu écris donc que ton équation est : (x² - 8x + 16) - 4 = 0
ce qui ne change rien à ton résultat, mais, sous cette forme, tu pourras trouver les solutions de l'équation ...
Qu'en penses-tu ?
Je voulais voir ce que tu allais répondre ?
Ce que tu as écrit est la bonne réponse...^
Alors je te laisse continuer !
donc (x-4)²-4=0
x-4=O soit x=4
Donc les solutions c'est le singleton 4, car -4 ne peut pas être solution ici.
Dommage !.... (x-4)² - 4 n'est pas x-4 !...
L'équation devient : (x-4)² - 2² = [(x-4)-2)]*[(x-4)+2] = 0
soit les 2 (bonnes) solutions ....
Tu termines ...
Tu me fais rire ... Relis l'énoncé, et vérifie si tout est fait, et bien fait !...
Pour la conclusion, tu peux développer un peu ce que je t'ai écrit ci-dessus.
Est-ce que tu avais une hypothése, une conjecture, avant de faire les calculs, sur la possibilité d'un angle droit en M , et sur sa position ?...
Ah ah ah ...
Chloé, Chloé ...
Je t'avoue que Mr.Duret des fois il met des DM super durs. Mais est ce une raison pour aller chercher la réponse sur le NET ?
C'est bien ce que je me disais.
Merci beaucoup, tu as du t'armer de patience pour m'aider 
Euh pour la question, je suis pas sur d'avoir bien compris ...
Et bien comme ma moyenne ne vole pas haut cette année, j'aimerai beaucoup avoir une note qui remontera cette dernière. ET puis c'est bien un devoir MAISON ? On peut s'aider de différents outils non ?


