Inscription / Connexion Nouveau Sujet
triangle dans un arc de cercle
Bonjour,
je suis très embarrassé par un exercice.
Est-ce que quelqu'un pourrait m'aider ?
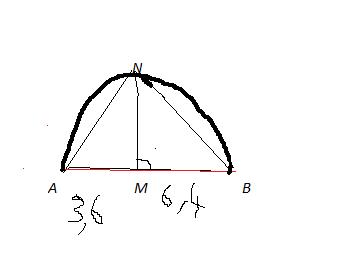
Il s'agit d'un triangle ABN dont un coté, l'hypoténuse (AB) est un diamètre de son cercle circonscrit, on en déduit que c'est un triangle rectangle.Ce triangle ANB est "divisé" en 2 : un segment coupe le triangle ANB à l'angle droit (l'angle N) jusqu'au point M qui appartient à (AB)
AM = 3,6 cm
MB = 6,4 cm.
Mon problème est que je n'ai qu'1 seul côté et je dois calculer AN ainsi que l'angle BAN
Voici l'énoncé :
determiner la valeur exacte de AN ; en déduire une valeur approchée de la mesure de l'angle BAN
D'avance, merci
Alors MN est la hauteur du triangle rectangle ABN en N donc d'après Pythagore MN² = ...x... En déduire MN.
Ensuite calcule AN et BN avec Pythagore.
merci, mais tu ne dois pas avoir fait le même dessin que sur mon livre, car sur mon livre, MN n'est pas l'hypoténuse, on ne peut donc pas appliquer pythagore.
Oui MN n'est pas l'hypoténuse et elle ne doit pas l'être pour pouvoir appliquer Pythagore , il suffit d'avoir un triangle rectangle !
Je suis d'accord, MN n'est pas forcément l'hypoténuse mais la formule doit être MN² + MB² = NB²
MN² +6,4² =NB²
Je n'ai donc pas assez d'informations
Merci de prendre du temps pour moi, mais je ne trouve pas comment calculer MN ? Je n'ai pas de valeurs sauf une : 6,4 cm
Ce n'est pas suffisant.
BONJOUR ,
J'ai le même exercice, je pense qu'il faut calculer avec les cosinus pour plus d'information livre de maths 4° page 97 n°77.merci pour votre aide.
excusez moi l'exercice c'est page 244 n°58 désolée pour l'erreur mais je pense qu'il faut utiliser le calcul avec les cosinus .
c'est sur il faut utiliser les cosinus mais d'abord calculer la hauteur du triangle, c'est a dire NM et on a pas assez d'informations pour le faire...
Désolé nos mails se sont croisés..
Personnellement je ne savais que l'on pouvait appliquer cette règle .
Merci beaucoup
Bonsoir Mathoumatheux ,
ton titre dit "Triangle dans un arc de cercle". Sur ce point-là on est bien d'accord.
 Cependant tu n'as pas mentionné une seule fois ce cercle dans ton énoncé alors je voudrais bien que tu m'écrives tout ce qui est écrit sur ton livre s'il te plaît. Merci d'avance.
Cependant tu n'as pas mentionné une seule fois ce cercle dans ton énoncé alors je voudrais bien que tu m'écrives tout ce qui est écrit sur ton livre s'il te plaît. Merci d'avance.  (Ceci n'était qu'une petite parenthèse CAPITALE !)
(Ceci n'était qu'une petite parenthèse CAPITALE !)
Mais revenons à nos "moutons" :
J'ai suivi ton énoncé à la lettre, reproduis la figure et voici ce que j'en pense :
Il est malheureusement impossible que l'angle AMN(ou BMN) soit un angle droit ! 
OU autre hypothèse,
ANB n'est pas un angle droit ! 
Voilà. Alors je voudrais que tu réécrives tout depuis le début même si tu la déjà fait.
Merci et bonne soirée. 
Voilà ce que j'ai compris :
ANB est un triangle rectangle en N et MN est son hauteur issue de N.
AM = 3,6 cm et BM = 6,4 cm
Bonsoir Michou946,
Je vais recopier EXACTEMENT ce qu'il est écris sur mon livre :
1) Construire en vraie grandeur la figure ci contre dans laquelle :
le point M appartient au segment AB
Le point N appartient au demi cercle de diamètre AB
2)Déterminer la valeur exacte de AN
3)En déduire la valeur approchée de la mesure de l'angle BAN
________________________________________________________________________________
J'ai bien écris " triangle dans un arc de cercle" comme titre mais pour moi, ce cercle ne servait qu'à montrer ,sans l'indiquer directement, que le triangle ANB est rectangle en N
Quant au triangle NMA, il est obligatoirement rectangle car sur mon dessin figure le codage l'indiquant.
Merci
DemoGeneral, merci de m'aider, en suivant vos indications, j'obtiens 8,4
et je fais l'inverse cosinus de l'angle A, cela me donne 64,62....° = (environ)
64,6°.
Seul petit problème, sur mon dessin (que j'ai fait en vraie grandeur (évidemment)) l'angle fait 53°.Mais peut-être que mon dessin n'est pas correct
J'ai bien peur de passer pour un idiot mais qu'est ce que c'est le "projeté orthogonal"
Dans tous les cas, M appartient au segment AB
DemoGeneral,
je n'ai pas compris ce que vous vouliez dire par "projeté orthogonal", pourriez vous m'expliquer ?
Est-ce que la fin de mon raisonnement semble correcte ?
Puisque je n'ai plus de réponse, je vais me déconnecter.Mais je voudrais remercier DemoGeneral pour m'avoir accordé du temps et pour m'avoir conduit sur le bon chemin.Merci.
Bonsoir

Excusez-moi Matoumatheux , je me suis déconnecté pour des raisons urgentes.
En tout cas H est le projeté orthogonal d'un point A sur une droite Delta veut dire que AB est perpendiculaire à Delta et B appartient à Delta.
Bonjour Matoumatheux (cette fois-ci je ne me suis pas trompé dans l'orthographe  )
)
Je suis désolée de ne pas t'avoir répondu hier soir mon ordinateur avait un problème  . Bref, à vrai dire je ne sais moi non plus ce que veut dire "projeté orthogonal".
. Bref, à vrai dire je ne sais moi non plus ce que veut dire "projeté orthogonal".
Mais revenons en à notre figure. Je me demandais si on pouvais metttre le point N n'importe où sur le demi-cercle.
Merci de me le préciser si tu le peux et bonne journée! 
bonjour a tous .
voici approximativement le dessin du livre.
j'ai déduis que M est un angle droit de 90°, a partir de là, j'ai fait le calcul en prenant 90°et la mesure de MB pour trouver l'angle de B j'ai en résultat 37°,pour A 63° et pour N53°pour l angle a droite et 27°pour son angle a gauche au total N=80° .
résultat l'angle BAN=63° en espérant que je n'ai pas fait d'erreurs? SI c'est le cas dites le moi merci
Voilà comment calculer BN et AN ( Puisque vous ne connaissez pas la règle que j'ai dit avant je vais le démontrer ):
MN² = BN² - MB²
MN² = AN² - AM² donc BN² - MB² = AN² - AM²
signifie AB² - AN² - MB² = AN² - AM²
AB² - MB² + AM² = 2AN²
(AM + BM)² - BM² + AM² = 2AN²
AM² + BM² + 2AM x BM - BM² + AM² = 2(MN² + AM²)
2AM² + 2AM x BM = 2MN² + 2AM²
2AM x BM = 2MN² on simplifie en multipliant par 1/2 et on obtient
AM x BM = MN²
maintenant on peut calculer MN et puis grace à Pythagore on calcule AN et BN.
bonjour DemoGeneral,
j essai de comprendre mais je n'arrive pas a calculer MN POUR POUVOIR me servir de Pythagore pour ANetBN MERCI DE M EXPLIQUER PAR L4INTERM2DIAIRE DE MATOUMATEUX.
MN² = AM x BM = 3,6 x 6,4 = 876/25
Selon Pythagore dans AMN on a AN² = AM² + MN²
AN² = (3,6)² + 876/25 = ... Tu fais des calculs normales et même chose pour BN.
Bonjour à tous,
voilà avec toutes vos données j'ai pu faire la figure. La voici 
C'est tout ce que je peux faire pour l'instant. 


