Inscription / Connexion Nouveau Sujet
Etude d'une suite un+1=racine(2-un)
Bonjour,
J'essaye d'étudier la suite un+1=racine(2-un) avec u0 inconnue mais je bloque.
Ds un premier temps j'ai essayé d'étudier la fonction f(un)=un+1 qui est décroissante sur ]-infini;2] mais ensuite je n'arrive pas vraiment à continuer. Il faut probablement étudier trois cas selon les valeurs de uo?
Pour l'étude du point fixe je trouve -2 et 1...
Bonjour
C'est déjà nécessaire d'avoir des quantités positives sous la racine... Donc déjà
Ensuite, -2 n'est pas point fixe!
Donc commence par regarder pour quels x on a f(x) < 2, ce qui te limitera les possibilités pour ...
Ensuite, -2 n'est pas point fixe!
pour quels x on a f(x) < 2
(piège classique... racine parasite après une élévation au carré)
Oui, de toute façon, pour que la suite existe c'est nécessaire d'avoir . Maintenant tu montres par récurrence, que cette condition assure l'existence de TOUTE la suite.
Bonjour,
J'imagine que tu as résolu l'équation x=racine(2-x)
Fais attention, les termes sont positifs à partir de U1
Observe que la suite (u_n) n'est pas définie si u_0<-2
Si u_0=-2 u_1=2 et ensuite u_n>0 -2 n'est pas un point fixe.
1 est point fixe ok
1 est le seul point fixe.
Observe la fonction f(x)=racine(2-x) et travaille avec la fonction id(x)=x
C'est classique On a f'(1)=-1/2 c'est important .
Montre que si u_0 appartient à [-2,2] u_n converge vers 1
Je viens de réussir la récurrence, j'ai utilisé la fonction f(un)=un+1 sachant qu'elle est décroissante sur ]-infini;2]
Ok donc
Donc on a f([-2;2]) inclue dans [0;2]
Et f est contractante sur [-2;2]
Et f a un point fixe 1 qui appartient à [-2;2]
Donc (un) avec u0 appartient à [-2;2] converge vers 1
C'est bien ça?
Et maintenant pour connaître la monotonie je dois sans doute faire des cas suivant les u0 possible non?
Oui, ça tend vers 1. Je ne vois pas pourquoi tu veux faire la monotonie... De toute façon avec une fonction décroissante ça fait un escargot...
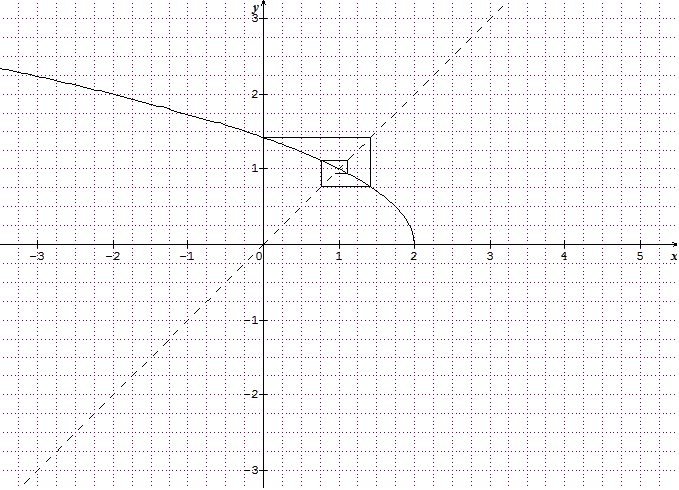


 analyse en post-bac
analyse en post-bac