Inscription / Connexion Nouveau Sujet
Prouver la fonction du discriminant/ équation second degré
J'ai mis programme de première parce que je ne crois pas que l'on fasse ça en seconde, par contre je suis incapable de dire le chapitre correspondant (donc si qqun peut me le dire pour ma culture 
)
Bon alors voilà je suis allée sur internet pour voir ce que c'était ces fameuses équations du second degré, vu qu'en seconde on en parle comme si c'était le saint graal réservé aux plus grands génies de la terre, et je suis tombée sur ça :
Équations du second degré.
Les équations du second degré sont simples mais il faut apprendre les différentes formules.
Avant de donner les formules on va définir ce qu'est une équation du second degré.
c'est une équation de la forme ax²+bx+c=0 (avec a non nul)
Pour pouvoir résoudre une telle équation il faut tout d'abord calculer le discriminant Δ.
Pour le calculer il est facile, il suffit d'appliquer cette formule :
Δ = b² - 4ac
On le calcule, ensuite selon le résultat on va pouvoir savoir le nombre de solutions qu'il y a, et les trouver s'il y en a.
Si Δ < 0 , rien de plus simple : il n'y a pas de solution.
Si Δ = 0, il y a une seule solution à l'équation : c'est x= -b/2a
Si Δ > 0 il y a deux solutions qui sont x1 = (-b-√Δ)/2a et x2= (-b+√Δ)/2a
Je n'aime pas voir des choses sans savoir expliquer le pourquoi du comment. je pense être capable d'appliquer bêtement cette formule mais j'aimerai savoir.
Quel est le rôle du discriminant et SURTOUT comment peut on le démontrer? Comment en gros on peut démontrer que Δ = b² - 4ac? j'ai cherché "démonstration discriminant" sur google mais ça n'a rien donné ^^
Et puis, comment démontrer les solutions? C'est à dire toute la dernière partie avec Δ < 0 , Δ = 0,Δ > 0?
Mais je pense que comprendre le discriminant m'aiderai bien, je crois qu'on entend aussi parler du discriminant dans les fonctions mais ma question ne porte pas sur ça 
(possible que je me trompe)
Bonsoir
ax²+bx+c=0
on divise par a
x²+bx/a+c/a=0
tu remarques que
x²+bx/a c'est le début de (x+b/2a)²=x²+bx/a+b²/4a²
donc x²+bx/a=(x+b/2a)²-b²/4a²
et
x²+bx/a+c=(x+b/2a)²-b²/4a²+c/a=0
=(x+b/2a)²-(b²-4ac)/4a²=0
si b²-4ac est >0 tu peux considérer l'expression ci dessus comme la différence de deux carrés
A²-B²
et les racines sont donc A=B et A=-B
A=x+b/2a
B=
(b²-4ac)/2a
si b²-4ac est <0, cette expression n'a pas de racine réelle et l'équation n'a pas de racines
Bonsoir.
Ceci figure dans le chapitre des polynômes [du second degré].
Comment en sommes-nous arriver à ce que nous appelons discriminant ?
On cherche la/les racine(s) du trinôme ax2 + bx + c.
Afin de trouver cette/ces racine(s), une solution est de factoriser.
En voici une démonstration :
f(x) = ax² + bx + c
=
Ici, nous sommes "bloqués", c'est-à-dire que factoriser d'avantage sous cette forme n'amènera à rien. On va donc chercher à "forcer" l'apparition d'une identité remarquable.
En ajoutant , on ne change rien (car ceci est égal à 0), donc :
Tu peux remarquer que (les trois premiers termes de la paranthèses) est le développement d'une identité remarquable. Je pense que tu peux la trouver aisément, donc :
Développons l'avant dernier terme :
Réduisons au même dénominateur l'avant et le dernier terme.
Voici. On appelle discriminant du trinôme le nombre réel 
= b² - 4ac, c'est-à-dire :
Ceci est appelé forme canonique du trinôme, tu en verras une partie en seconde.
__________
Si tu arrives à suivre jusque-là, c'est déjà pas mal. Passons à la résolution de cette équation. Pour cela, prenons le résultat trouvé précédemment.
Il faudra traiter 3 cas différents :
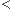0
0
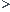= 0
_________
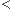Si 0
On a :
a2 est toujours positif car c'est un carré.
On a supposé < 0 donc forcément, - > 0. Au final, on obtient :
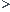0
D'autre part
0 (car c'est un carré)
On a donc la somme d'un terme supérieur ou égal à 0 et d'un terme strictement supérieur à 0 :
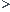0 donc
0
Comme on a, a 0, on a donc :
0
f(x) 0
Donc lorsque 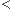0, il n'y a aucune racine réel.
________
Si = 0
Puisque on a supposé = 0, 0 divisé par n'importe quelle nombre sauf 0 est égal à 0. On a donc :
= 0
= 0
= 0
x =
lorsque = 0, il n'y a donc qu'une seule racine.
________
Si 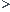0
Ici, on va chercher à utiliser l'identité remarquable a² - b². On peut écrire = (2)
=
=
On a une forme a2 - b2. Donc :
=
Regroupons les mêmes dénominateurs, on obtient :
= 0
Je pense que tu peux deviner la suite.
Voilà
Bonjour,
L'idée est de mettre l'équation sous une forme qu'on appelle canonique :
Tout d'abord, a étant 0, on peut tout diviser par a :
x² + (b/a)x + c/a = 0
Ensuite, on remarque que x² + b/a est le début d'un carré, plus précisément on a :
(x + b/2a)² = x² + (b/a)x + b²/(4a²)
Et donc :
x² + (b/a)x = (x + b/2a)² - b²/(4a²)
Et donc :
(x + b/2a)² - b²/(4a²) + c/a = 0
Ou encore :
(x + b/2a)² - (b²-4ac)/(4a²) = 0
Et voici le delta qui apparaît, je vais le noter D :
D = b²-4ac
et donc :
(x + b/2a)² - D/(4a²) = 0
Maintenant, il y a 3 cas :
D < 0, donc (x + b/2a)² - D/(4a²) > 0, donc pas de solution à x + b/2a)² - D/(4a²) = 0
D = 0, donc (x + b/2a)² = 0, donc x + b/2a = 0, donc x = -b/2a
D > 0, alors D existe, et l'équation devient :
(x + b/2a)² - (D/(2a))² = 0
Equation qui est de la forme A²-B² = (A+B)(A-B), d'où
((x + b/2a) + D/(2a))((x + b/2a) - D/(2a)) = 0
d'où les solutions :
x1 = (-b + D)/(2a)
x2 = (-b - D)/(2a)
Voila voila...
Annuler
connectez vous