Inscription / Connexion Nouveau Sujet
Parallélépipède rectangle
Bonjour a tout le monde,
Je bloque sur le parallélépipède rectangle car je n'est pas encore vu ses propriétées.
Je galère aussi en géométrie, merci de votre comprhénsion.
Enoncé:
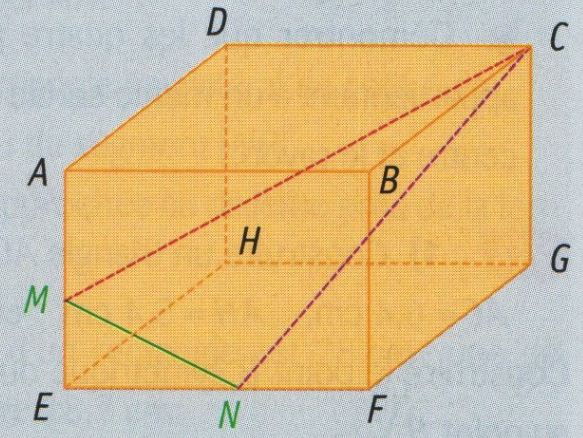
ABCDEFGH est un parallélépipède rectangle tel que : -AB = 7 cm et FG = 6 cm
-M appartient à [AE] et AM = 3 cm
-N appartient à [FE] et NF = 3 cm
Questions:
1) Calculer MN2
2) a)Calculer AC2
b)En considérant le triangle rectangle AMC, calculer MC2
3) Calculer NG2 puis NC2
4) Le triangle MNC est-il rectangle ?
Bonjour a tout le monde,
Je bloque sur le parallélépipède rectangle car je n'est pas encore vu ses propriétées.
Je galère aussi en géométrie, merci de votre comprhénsion.
Enoncé:
ABCDEFGH est un parallélépipède rectangle tel que : -AB = 7 cm et FG = 6 cm
-M appartient à [AE] et AM = 3 cm
-N appartient à [FE] et NF = 3 cm
Questions:
1) Calculer MN2
2) a)Calculer AC2
b)En considérant le triangle rectangle AMC, calculer MC2
3) Calculer NG2 puis NC2
4) Le triangle MNC est-il rectangle ?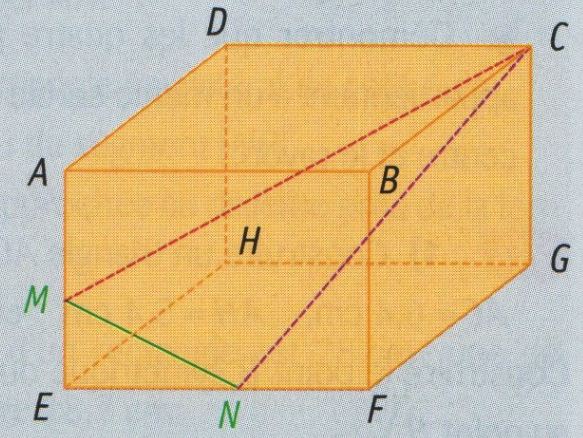
*** message déplacé ***
* Océane > le multi-post n'est pas toléré sur le forum ! *
pour calculer MN², il faut te placer dans le triangle MNE rectangle en E et utiliser pythagore
Pour le calcul de AC², il faut utiliser pythagore dans le triangle ABC rectangle en B
Pour NG², idem dans le triangle NGF rectangle en F
et NC² dans le triangle NFC rectangle en F
ne pas oublier qu'il s'agit d'un parallélépipède rectangle, donc AB=EF=DC=GH et AE=BF=CG=DH et AD=BC=EH=FG
*** message déplacé ***
Pour MN2 J'ai compris
En revanche je comprend pas trop les suivantes:
Pour AC 2 aucune droite ou segment passe par [AC]
Pour NG 2 aucune droite ou segment passe par [NG]
Pour NC 2 aucune droite ou segment passe par [CF]
Merci de me répondre :p
*** message déplacé ***
trace les segments qu'il te manque. ce n'est pas parce qu'ils ne sont pas tracés qu'ils n'existent pas
*** message déplacé ***
bonjour,
c'est Pythagore partout ...
tu dois trouver les triangles rectangles utiles (tracés ou non sur ta figure)
par exemple pour trouver AC, tu vas utiliser le triangle ABC ou ADC au choix
bonjour,
je vois que je ne suis pas le seul à penser qu'il manque une donnée!
ce serait bien que geoffrey311 confirme son énoncé sinon son problème est insoluble...
En effet il manque AE = 5 cm.
Rayliz ==> Quelle propriétée a tu utilisée pour savoir que EN = AB - 3 = 4 cm
1) On sait que AB=7cm et toutes les faces du parallélépipède sont des rectangles
Or si un quadrilatère est un rectangle alors ses côtés opposés sont de même longueur.
Donc AB = EF = 7 cm
On sait que MNE triangle rectangle en E tel que ... Là je bloque parceque je sais pas quelle longueur font ME et EN
Haaa je viens de réfléchir !
Avant le 2eme chainon il fallait faire une parenthèse et dire que
EN = AB-3=4cm
et
ME=AE-AM
AE=AE-3 cm
1) On sait que AB=7cm et toutes les faces du parallélépipède sont des rectangles
Or si un quadrilatère est un rectangle alors ses côtés opposés sont de même longueur.
Donc AB = EF = 7 cm et AE = BF = 5 cm
On sait que ABEF est un rectangle et AB = EF = 7cm et AE = BF = 5cm
AE=ME+AM
5=ME+3
5-3=ME
EF=EN+NF ME = 2 cm
7=EN+3
7-3=EN
EN=4cm
On sait que MNE triangle rectangle en E tel que EN = 4cm et ME = 2cm
Or d'après le théorème de Pythagore
On a MN=ME+EN
MN=2+4
MN=4+16
MN=20
MN est le nombre positif dont le carré vaut 20
Donc V20
= approximativement 4.47
quelques corrections en gras!!!
On sait que MNE triangle rectangle en E tel que EN = 4cm et ME = 2cm
Or d'après le théorème de Pythagore
On a MN²=ME²+EN²
MN²=2²+4²
MN=4+16
MN=20
MN est le nombre positif dont le carré vaut 20
Donc MN=V20
= approximativement 4.47
attention il lui est demandé que des valeurs au carré car je ne pense pas que geoffrey311 connaisse les racines carrés en 4eme?....
une étourderie en recopiant :
On a MN²=ME²+EN²
MN²=2²+4²
MN=4+16 <- c'est MN2 = 4 + 16
MN=20 <-- c'est MN2 = 20
salut,
bien que ce soit Noel, ce ne serait pas un cadeau que de te donner toutes les réponses sans que tu ne proposes rien...
toutes les questions sont des applications de Pythagore la dernière question étant la réciproque..
AC²:triangle ADC ou ABC
envoie ton résultat et Joyeux Noel
Salut, J'espere que vous avez passez de bonnes fêtes de Nawel 
2)a)On sait que ABC est un triangle rectangle en B tel que AB=7cm et CB=FG=6cm et [AC] est l'hypoténuse
D'apres la définition du théoreme de Pythagore.
On a AC²=AB²+BC²
=7²+6²
=49+36
=85
AC est le nombre positif dont le carré vaut 85
Donc AC=V85
= approximativement 9,21
2)b)
On sait qu AMC triangle rectangle en A tel que AC²=85 et AM=3cm et MC est l'hypoténuse.
Or d'apres le théoreme de Pythagore
On a MC²=AC²+AM²
=85+3²
=85+9
MC²=94
MC est le nombre dont le carré vaut 94
Donc MC=V94
= approximativement 9.69
3)NG²
On sait que NFG triangle rectangle en F tel que NF=3cm et FG=6cm et NG est l'hypoténuse
Or d'apres le théoreme de Pythagore
On a NG²=NF²+FG²
=3²+6²
=9+36
NG²=45
NG est le nombre positif dont le carré vaut 45
Donc NG=V45
= approximativement 6.70
ok Merci
Je reprend
3) NC²
On sait que NGC est un triangle rectangle en G tel que CG=AE=5cm et NG=FG=6cm et NC est l'hypoténuse
Or d'apres le théoreme de Pythagore
On a NC²=CG²+NG²
=5²+6²
=25+36
NC²=61
NC est le nombre positif dont le carré vaut 61
Donc NC=V61
= approximativement 7.81
Oups
On sait que NGC est un triangle rectangle en G tel que CG=AE=5cm et NG²=45 et NC est l'hypoténuse
Or d'apres le théoreme de Pythagore
On a NC²=CG²+NG²
=5²+45
=25+45
NC²=70
NC est le nombre positif dont le carré vaut 70
Donc NC=V70
= approximativement 8,36

remarque : dans ton texte on ne te demande que les carrés MN², MC², NC², ... ; pas les valeurs de MN ou NC ...
Re-bonjour à tout le monde;
4)
Calculs:
Carré du plus grand côté: MC² = 94
Somme des carrés des deux autres côtés :
MN² + CN² = 20 + 70
MN² + CN² = 90
On sait que dans le triangle MNC,
On a MC² pas égal à MN² + CN²
Si le triangle RST était rectangle en N
alors d'apres le théoreme de Pythagore
on aurait MC² = MN² + CN² <===== Ce n'est pas le cas
Donc MNC n'est pas un triangle rectangle.

Merci de me corriger ! 
J'ai un doute par rapport a ce chainon :
On sait que AB=7cm et toutes les faces du parallélépipède sont des rectangles
Or si un quadrilatère est un rectangle alors ses côtés opposés sont de même longueur.
Donc AB = EF = 7 cm
Ne manque t-il pas d'autres réponses dans le "Donc" ?
si tu as juste besoin de EF c'est suffisant
si après tu as besoin de BF, tu peux ajouter "et AE = BF = 5 cm"
ok Merqui encore et encore.
Je vais recopier tout ça au propre pour un petit 10/10 [...] enfin j'espere !












