Inscription / Connexion Nouveau Sujet
Fonction dérivée 1S
Bonjour,
Voici l'énoncé de mon exercie.
On veut réaliser un toboggan pour les enfants, qui se termine en pente douce.
Il doit donc vérifier les conditions suivantes:
1) avoir une tangente au point A parrallèle au sol
2) être tangent au sol au point B
Dans tout le problème, on considère le plan rapporté au repère orthonormé (Oij)
A(0;2)et B(4;0) avec la courbe passant par (2;1).
Cf figure .
Le but du problème est de trouver des fonctions dont les courbes représentatives ont l'allure du toboggan et vérifiant les conditions de l'énoncé.
1) Une fonction polynome du premier degré peut-elle convenir? Expliquer pourquoi?
2a) f est une fonction définie sur [0;4] par f(x)= -1/4x²+2 et Cf sa courbe représentative dans (Oij). Etudier les variations de f et dresser son tableau de variation.
2b) g est la fonction définie sur [0;4] par g(x)=1/4x²-2x+4 et Cg sa courbe représentative dans (Oij). Etudier les variations de g et dresser son tableau de variation.
2c)Démontrer que C et Cg, ont en commun le point C de coordonnées (2;1)
2d) Démontrer que C et Cg ont la même tangente T au point C.
2e) Tracer T, puis Cf et Cg sur un même graphique.
Ensuite tracer d'une couleur différente, les deux portions des courbes Cf et Cg représentant le toboggan.
2f)vérifier que la courbe obtenue satisfait aux conditions (1) et (2).
3) On décide de donner au toboggan un profil correspondant à la courbe représentative dans (Oij) d'une fonction polynome (P) du 3ème degré: P(x)=ax^3+bx²+cx+d
3a) Trouver la valeur de d sachant que la courbe passe par A.
3b)Sachant que la courbe doit vérifier les conditions (1) et (2) et qu'elle passe par B, trouver les valeurs de a, b et c.
3c) h est la fonction définie sur [o;4] par h(x)= 1/16x^3-3/8x²+2
Etudier les variations de h et donner son tableau de variation.
3d) Sur un nouveau graphique, tracer Ch représentant h dans (O; i,j)
4) Observer les graphiques, puis calculer la pente maximale ( c'est-à-dire le maximum de I f'(x) I ) du toboggan dans chacun des deux cas étudiés et conclure sur le cas le plus favorable.
Merci
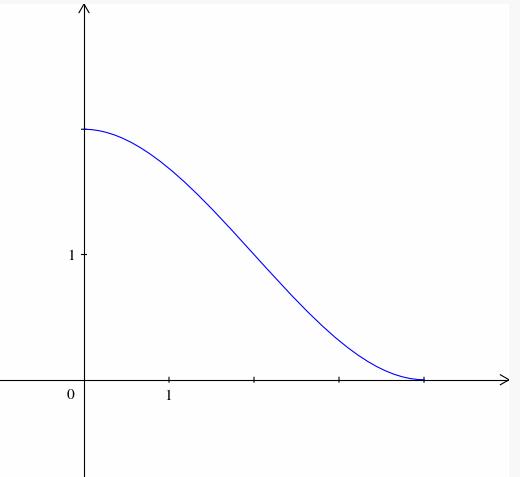
bonjour,
as-tu cherché?
si une fonction f convient la courbe correspondante admet des tangentes en A et B donc la fonction est dérivable en x=0 et en x=4 et en ces points les nombres dérivés sont nuls f'(0)=f'(4)=0
1)une fonction du premier degré en x est représentée par une droite ,dans ce cas les points A et B étant sur le toboggan le toboggan serait représenté par le segment de droite AB qui ne vérifie pas les conditions imposées
il n'est pas tangent au sol en B et n'admet pas en A une tangente parallèle au sol
la fonction f correspondante a pour expression f(x)=ax+b
A est sur le toboggan<=>2=a.0+b donc b=2
B est sur le toboggan<=>0=a.4+2=>a=-
donc
on a bien donc C est sur le toboggan mais les conditions sur les tangentes en A et B ne sont pas vérifiées puisque f'0)=f'(4)=-
tu continues
bonsoir,
Je suis désolé j'avais oublié de posté ce que j'ai fait.
Merci de votre réponse je vais comparer avec se que j'ai fait et posterai le reste.
Merci
Voici ce que j'avais déjà fait.
1- Je pense qu'une fonction polynôme du premier degrés ne peut pas convenir car elle n'admet pas de tangente.
2-(a)f est négatif sur [0;4]
f'(x)=x/2 négative sur l'intervalle de définition donc décroissant sur l'intervalle de definition.
(b)g est négatif sur [0;4]
g'(x)=x/2-2 s'annule pour x=4
(c)Le point C est tel que f(x)=g(x) => (-1/4)x²+2=(1/4)x²-2x+4=0
=>x=2 et donc le point commun a pour coordonnées [2;f(2)={2;1}]
Pourriez-vous me dire si cela est correct?
Merci encore
pour la première question:
une fonction polynôme du premier degré est représentée par une droite ,elle a une tangente en chaque point c'est elle même mais le texte impose des tangentes //x'ox en A et en B c'est cela qui n'est pas possible
f(x)=ax+b=>f'(x)=a le nombre dérivé est constant f'(0)=0=>a=0 mais alors f(x)=b donc b=f(0)=4 et b=f(2)=0 c'est donc impossible
2)
a)
f'(x)= tu as oublié de taper le -
f'(0)=0=>tangente //x'ox en A
f'(x) est donc négative sur [0;4]=> f est décroissante
b)
g'(x) 0 sur [0;4] tu as oublié le '
0 sur [0;4] tu as oublié le '
g'(4)=0 c'est d'accord donc en B(4;0) la tangente à la courbe représentant g est portée par x'ox
c) le point commun aux deux courbes est bien C(2;1)
d)en C f'(2)=-1 et g'(2)=-1=> en ce point les deux courbes ont la même tangente de coefficient directeur -1
tu continues
Bonjour,
je n'ai pas compris cette expression "//x'ox".
Pourriez-vous me l'expliquer .
Merci d'avance
Pour la 2 b) la fonction g'(x) est positif et donc elle est décroissante sur [4;0]
Est-ce correct?
Merci
Bonjour,
Pourriez-vous m'aider pour la (e), je ne comprends pas pourquoi mes deux courbes n'ont pas le point commun.
Merci
//x'ox cela veut dire parallèle à x'ox l'axe des abscisses
2)b
g'(x)<0 sur [0;4[ et g'(4)=0 sur[0;4] g décroit de 4 à 0
g est décroissante sur [0;4]
x |....0....... 2 ......4
g'(x)|...-2......-1........0
g(x) |....4.......1........0
Bonjour,
Pour la (e), si j'utilise le logiciel géogébra, que dois-je écrire alors pour pouvoir faire les deux courbes et voir le point commun?
Merci
je ne sais pas,je n'utilise pas de logiciel
tu peux très bien tracer les courbes à la main,ce sont des arcs de paraboles
si x est l'abscisse d'un point commun aux deux courbes x est solution de f(x)=g(x) soitsoit
C (2;1) est le seul point commun aux deux courbes
Bonsoir,
Pourrai-je avoir des explications s'il vous plait, pour la (e) je ne comprends pas comment faire?
Merci
bonsoir,
quand tu as tracé les courbes représentatives de f et g
tu remarques que:
*l'arc de pour 0
 x
x 2 ne peut pas appartenir au toboggan puisqu'il passe par le point (0,4)
2 ne peut pas appartenir au toboggan puisqu'il passe par le point (0,4)
par contre l'arc de convient sur cet intervalle,il passe par A(0;2),en ce point le nombre dérivé est nul donc on a bien une tangente //x'Ox et pour x=2 f(x)=1
*sur l'intervalle [2,4]
l'arc de correspondant ne peut convenir il ne passe pas par le point (4;0)
par contre l'arc de correspondant convient,il passe parB(4;0) et est tangent en B à x'Ox
donc le toboggan est représenté par
f pour 0 x
x 2
2
g pour 2 x
x 4
4
les deux arcs de courbes passent par le point (2,1),en ce point les deux courbes ont la même tangente T
ce sont ces deux arcs de courbe que tu dois tracer en rouge par exemple pour montrer qu'ils représentent le toboggan
Bonjour,
Est-ce que cela est correct?
3-(b)
Le toboggan doit avoir une tangente en A parallèle au sol.
P'(0)=0 ce qui donne c=0 et l'équation de la tangente doit être y=2
P(0)=2, ce qui confirme que d=2
Il doit être tangent au sol au point B {4,0}.
P'(0)=0 l'équation de la tangente doit être y=0
P'(4)=0 <=> 3*16*a+2*4*b=0 <=> 8(6a+b)=0 ... (Je ne sais pas si c'est bon ou pas =\
6a+b=0 <=> b=-6a
La courbe passe par B:
P(4)=0 <=> 64*a+16*b+2=0 <=> 64*a+16*(-6*a)+2=0 <=> a=1/16
64*1/16 + 16*b + 2=0 <=> 6 + 16*b =0 <=> b= -3/8
Merci d'avance


