Inscription / Connexion Nouveau Sujet
exercice de maths 2
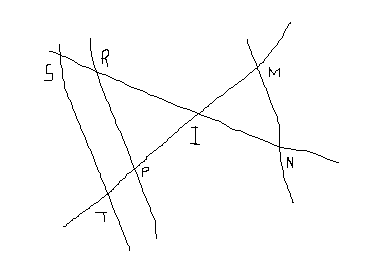
Dans ce dessin : ***
-les points M, I, P et T sont alignés
-les points N, I , R , S sont alignés
-RP et ST sont parallèles
- IS = 9cm ; IT = 12cm ; IR = 3cm
- RP = 5cm ; IM = 2.5cm et IN = 3cm
1. Démontrer que ST = 15cm
2. Tracer en vraie grandeur la figure complète
3. Les droites (MN) et (ST) sont-elles parallèles ? Justifier
4. Les droites (IT) et (IS) sont-elles perpendiculaires ? Justifier
Voici mes réponses :
Bonjour,
1. D'après Thalès : AK/AC = AG/AB = EF/BC
2.5/12 = 3/9 = 5/BC
3/9 = 5/BC produit en croix BC = 9*5 / 3 = 45/3 = 15 BC = 15cm
Donc BC = 15cm
2. J'ai tracé la figure
3. Je sais pas
4. Je sais pas
Dites moi si mes réponses sont bonnes svp, corriger moi et aider moi pour les questions que je n'arrive pas svp. Merci d'avance.
édit Océane
dans mon sujet et dans la partie Où j'en suis, dans MES RÉPONSES je me suis trompé dans les lettres voici les bonnes lettres :
1. D'après Thalès : IM/IT = IN/IS = RP/ST
2.5/12 = 3/9 = 5/ST
3/9 = 5/ST produit en croix ST = 9*5 / 3 = 45/3 = 15 ST = 15cm
Donc ST = 15cm
2. J'ai tracé la figure
3. Je sais pas
4. Je sais pas
Dites moi si mes réponses sont bonnes svp, corriger moi et aider moi pour les questions que je n'arrive pas svp. Merci d'avance.
1. D'après Thalès : IM/IT = IN/IS = RP/ST
ce ne sont pas les bons quotients....
les droites parallèles, au départ sont (RP) et (ST) donc les bons quotients sont
IR/IS = IP/IT = RP/ST
question 3 : utilise la réciproque du théorème de Thalès
question 4 : utilise la réciproque du théorème de Pythagore
je crois que la réciproque de thalès c'est : Soient deux droites (AB) et (AC) sécantes en A. Soit D un point de la droite (AB) distinct de A, et E un point de la droite (AC) distinct de A.
Si les points A, B et D d'une part, et A, C et E d'autre part sont alignés dans le même ordre.
Si , alors les droites (DE) et (BC) sont parallèles.
mais faut changer les lettres et j'y arrive pas je sais que je vais me tromper car j'arrète pas de confondre les lettres
Soient deux droites (AB) et (AC) sécantes en A. Soit D un point de la droite (AB) distinct de A, et E un point de la droite (AC) distinct de A.
Si les points A, B et D d'une part, et A, C et E d'autre part sont alignés dans le même ordre.
Si AB/AD=AC/AE , alors les droites (DE) et (BC) sont parallèles. : tu as oublié le plus important.....les quotients égaux
aaaaa oui désolé :
Soient deux droites (AB) et (AC) sécantes en A. Soit D un point de la droite (AB) distinct de A, et E un point de la droite (AC) distinct de A.
Si les points A, B et D d'une part, et A, C et E d'autre part sont alignés dans le même ordre.
Si , AD/AB = AE/AC alors les droites (DE) et (BC) sont parallèles.
mais il faut changer les lettres avec les lettres de mon triangle non ?
je n'y arrive pas il y a pleins de lettres, je n'arrête pas de confondre tu peux m'aider stp.
tu veux démontrer que les droites (MN) et (ST) sont parallèles
tu as donc les droites (SN) et (TM) qui se coupent en I
les points sont
I S N et
I T M
les quotients à calculer sont
IS/IT et IN/IM
s'ils sont égaux les droites (ST) et (MN) sont parallèles
s'ils sont inégaux les droites ne sont pas parallèles....à toi le calcul
oups...j'ai cliqué top vite, les bons quotients ne sont pas ceux que j'ai écrits, excuse moi 
je rectifie....
les points sont
I S T et
I N M
les bons quotients, cette fois-ci
IS/IN et IT/IM
excuse moi encore 
on veut démontrer que les droites (MN) et (ST) sont parallèles
on a donc les droites (SN) et (TM) qui se coupent en I
les points sont
I S N et
I T M
les quotients à calculer sont
IS/IT et IN/IM
D'après la réciproque de Thalès :
IS/IT et IN/IM
9/12 et 3/2.5
0.75 et 1.2
Ils ne sont pas égaux donc ils ne sont pas parallèles.
c'est sa ?
est ce que je dois marquer la définition de la réciproque de thalès :
Soient deux droites (AB) et (AC) sécantes en A. Soit D un point de la droite (AB) distinct de A, et E un point de la droite (AC) distinct de A.
Si les points A, B et D d'une part, et A, C et E d'autre part sont alignés dans le même ordre.
Si AB/AD=AC/AE , alors les droites (DE) et (BC) sont parallèles.
avec ta rectification j'ai refait :
on veut démontrer que les droites (MN) et (ST) sont parallèles
on a donc les droites (SN) et (TM) qui se coupent en I
les points sont
I S T et
I N M
les quotients à calculer sont
IS/IN et IT/IM
D'après la réciproque de Thalès :
IS/IN et IT/IM
9/3 et 12/2.5
3 et 4.8
Ils ne sont pas égaux donc ils ne sont pas parallèles.
c'est sa ?
est ce que je dois marquer la définition de la réciproque de thalès :
Soient deux droites (AB) et (AC) sécantes en A. Soit D un point de la droite (AB) distinct de A, et E un point de la droite (AC) distinct de A.
Si les points A, B et D d'une part, et A, C et E d'autre part sont alignés dans le même ordre.
Si AB/AD=AC/AE , alors les droites (DE) et (BC) sont parallèles.
Bonjour,
effectivement les droites (MN) et (ST) ne sont pas parallèles 
est ce que je dois marquer la définition de la réciproque de thalès :
ce n'est pas une définition, mais un théorème...
tu pourrais écrire par exemple :
"puisque IS/IN
 (IT)/(IM), toutes les conditions de la réciproque du théorème de Thalès ne sont pas remplies donc les droites (MN) et (ST) ne sont pas parallèles."
(IT)/(IM), toutes les conditions de la réciproque du théorème de Thalès ne sont pas remplies donc les droites (MN) et (ST) ne sont pas parallèles."pour la question 1. la réponse c'est :
Les droites parallèles au départ sont (RP) et (ST) donc les quotients sont: IR/IS = IP/IT = RP/ST (est ce que cette phrase je dois l'écrire ?répond moi stp)
D'après Thalès :
IR/IS = IP/IT = RP/ST
3/9 = IP/12 = 5/ST
3/9 = 5/ST
produit en croix : ST = 5*9/3 = 45/3 = 15
Donc ST = 15 cm
pour la question 3. la réponse c'est :
on veut démontrer que les droites (MN) et (ST) sont parallèles
on a donc les droites (SN) et (TM) qui se coupent en I
les points sont
I S T et
I N M
les quotients à calculer sont
IS/IN et IT/IM
D'après la réciproque de Thalès :
IS/IN et IT/IM
9/3 et 12/2.5
3 et 4.8
Ils ne sont pas égaux donc ils ne sont pas parallèles.
Puisque IS/IN et IT/IM, toutes les conditions de la réciproque du théorème de Thalès ne sont pas remplies donc les droites (MN) et (ST) ne sont pas parallèles.
Voila peux tu me dire si les réponses sont bonnes et peux tu m'aider pour la question 4. stp
pour le 4. la réponse c'est :
On veut démontrer que les droites IT et IS sont perpendiculaires. On a donc les droites..... après je sais pas enfait c'est la phrase que t'avais fait pour la question 3.mais est ce que je l'écris ou pas ?
D'après la réciproque de Pythagore :
1. IT² + IS²
12²+9²
144+81
225
2. ST² = 15² = 225
Donc d'après 1. et 2. et la réciproque du théorème de Pythagore SIT est rectangle en I et les droites IT et IS sont perpendiculaires.
C'est sa ?
ps : sur le dessin d'en haut c'est mal dessiné et on voit pas bien l'angle du triangle SIT mais sur ma feuille on le voit, quand je met mon équerre sa fait un angle droit.
peux tu corriger les réponses des trois questions que je viens de t'écrire stp. MERCI D'AVANCE.
tout d'abord réponse à ton dernier message :
tu ne dois pas commencer par "D'après la réciproque...."
voila comment tu peux rédiger correctement :
"Dans le triangle ITS on a :
IT² + IS² = 12²+9² = 144+81 = 225
et
ST² = 15² = 225
d'où IT² + IS² = ST²
donc, d'après la réciproque du théorème de Pythagore, le triangle TIS est rectangle en I et, par suite, les droites (IT) et (IS) sont perpendiculaires."
d'accord, il n'y a pas d'autres fautes dans ma réponse de la question 4 ? les calculs sont bons, la réponse est bonne...?
et peux tu corriger les réponses de la question 1. et 3. s'il te plait.( ils sont en haut de la réponse de la question 4.)
maintenant réponse à ton avant dernier message :
pour la question 1. la réponse c'est :
Les droites parallèles au départ sont (RP) et (ST) donc les quotients sont: IR/IS = IP/IT = RP/ST (est ce que cette phrase je dois l'écrire ?répond moi stp)
D'après Thalès :
IR/IS = IP/IT = RP/ST
3/9 = IP/12 = 5/ST
3/9 = 5/ST
produit en croix : ST = 5*9/3 = 45/3 = 15
Donc ST = 15 cm
tu peux rédiger comme cela :
"Les droites (RP) et (ST) sont parallèles donc, d'après le théorème de Thalès
IR/IS = IP/IT = RP/ST
3/9 = IP/12 = 5/ST
3/9 = 5/ST
ST = 5*9/3 = 45/3 = 15
donc ST = 15 cm."
pour la question 3. la réponse c'est :
on veut démontrer que les droites (MN) et (ST) sont parallèles
on a donc les droites (SN) et (TM) qui se coupent en I
les points sont
I S T et
I N M
les quotients à calculer sont
IS/IN et IT/IM
D'après la réciproque de Thalès :
IS/IN et IT/IM
9/3 et 12/2.5
3 et 4.8
Ils ne sont pas égaux donc ils ne sont pas parallèles.
Puisque IS/IN et IT/IM, toutes les conditions de la réciproque du théorème de Thalès ne sont pas remplies donc les droites (MN) et (ST) ne sont pas parallèles.
Tu peux rédiger comme cela :
"Les droites (SN) et (TM) se coupent en I
les points S, I, N et T, I, M sont alignés dans le même ordre
je calcule les quotients IS/IN et IT/IM :
IS/IN = 9/3 = 3
IT/IM = 12/2,5 = 4,8
donc IS/IN
 IT/IM.
IT/IM.
Puisque IS/IN
 (IT)/(IM), toutes les conditions de la réciproque du théorème de Thalès ne sont pas remplies donc les droites (MN) et (ST) ne sont pas parallèles."
(IT)/(IM), toutes les conditions de la réciproque du théorème de Thalès ne sont pas remplies donc les droites (MN) et (ST) ne sont pas parallèles."