Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. PremièreForum de première FonctionsTopics traitant de fonctions [tout]Lister tous les topics de mathématiques

1 2 3 +

Niveau première
Partager :

Problème: Aire d'un rectangle

Posté par
yoppyop 26-09-11 à 17:57

Bonjour, voila j'ai un exercice a faire mais je bloque dès la deuxieme question si vous pouviez m'aider a le résoudre ça serait vraiment cool

Voila le sujet:
  
   Le point M est situé sur un quart de cercle de centre O, de rayon 4 etr d'extrémités A et B. Le point N est le pied de la perpendiculaire à la droite (OA) passant par M. Le point P est le pied de la perpendiculaire à la droite (OB) passant par M.
On pose x=ON et on désigne par f(X) l'aire du rectangle ONMP.

1. Déterminer le domaine de définition D de la fonction f.

2. Montrer que, pour tout X de D, f(X)= xX16-x² .

3. a. Vérifier que, pour tout X de D, on a : f(X)= √64-(X²-8)²
   b. En déduire que le maximum de f vaut 8. En quelle valeur est-il atteint ?
   c. Que peut-on dire du rectangle ONMP lorsque son aire est maximale ?

4. a. A l'aide de la définition d'une fonction décroissante montrer que la fonction u(X)= (X²-8)² est décroissante sur l'intervalle [0 ; 2√2].
   b. En déduire le sens de variation de f sur [0 ; 2√2].
   c.Etudier les variations de f sur l'intervalle [2√2 ; 4]
   d. Construire le tableau de variations de f sur l'intervalle [0 ; 4].

5. Representer graphiquement la fonction f sur l'intervalle [0 ; 4].

Voila ce que j'ai trouver pour l'instant.

1. Df=[0 ; 4]
2. Dans OMN rectangle en N, on applique le théorème de Pythagore: OM²=ON²+NM²  NM²=OM²-ON²=16-X²  NM=√16-x²
De plus l'aire de OPNM est ONxNM donc X√16-x².

Pouvez vous m'aider a faire la suite
Merci

Posté par
Hiphigeniere : Problème: Aire d'un rectangle 26-09-11 à 19:08

Bonjour yoppyop

Pour le 3.a) tu développes  \sqrt{64-(x^2-8)^2} pour montrer que le résultat est bien égale à   x\sqrt{16-x^2}.

3.b) On a  :  f(x)=\sqrt{64-(x^2-8)^2}.

Le radicand  64-(x^2-8)^2 est une différence entre une constante (64) et une expression variable   (x^2-8)^2.

Quand une telle différence est-elle maximale ?
Que faut-il retirer à 64 pour que la différence  64-(x^2-8)^2  soit la plus grande possible ?

Quelle est alors cette valeur maximale pour la différence ?

Par conséquent, quelle est alors la valeur maximale pour f(x)=\sqrt{64-(x^2-8)^2}  ?

Posté par
yoppyopre : Problème: Aire d'un rectangle 27-09-11 à 07:40

Merci c'est bon j'ai prouver que 8 est le maximum et qu'il est atteint pour 2√2.
Maintenant a la 3. c je pense que c'est un carré lorsque son aire est maximale mais comment le prouver ?

Posté par
Hiphigeniere : Problème: Aire d'un rectangle 27-09-11 à 08:23

Dans ton premier post tu as écrit que NM=\sqrt{16-x^2}.

Comme tu as trouvé que l'aire maximale du rectangle était atteinte si x = 2\sqrt{2}, on a ainsi que ON = 2\sqrt{2} et NM = \sqrt{16-x^2} = \sqrt{16-8}=\sqrt{8}=2\sqrt{2}.

Ainsi, le rectangle ONMP est tel que ON=NM.

C'est donc un carré.

Posté par
Hiphigeniere : Problème: Aire d'un rectangle 27-09-11 à 09:07

On aurait pu également le prouver autrement.

L'aire maximale du rectangle vaut 8.
Un côté du rectangle mesure 2\sqrt{2}.

L'autre côté du rectangle mesurera   \large \frac{8}{2\sqrt{2}} = \frac{4}{\sqrt{2}} = \frac{4\times\sqrt{2}}{\sqrt{2}\times\sqrt{2}}= \frac{4\sqrt{2}}{2}=2\sqrt{2}

Posté par
yoppyopre : Problème: Aire d'un rectangle 27-09-11 à 21:02

Ok merci maintenant c'est bon j'ai fini mon sujet !

Posté par
Hiphigeniere : Problème: Aire d'un rectangle 27-09-11 à 21:05

C'est parfait alors !  

Bonne soirée  

Posté par
jeancmre : Problème: Aire d'un rectangle 29-10-11 à 12:23

avez vous compris les questions 1 et 2
merci

Posté par
jeancmre : Problème: Aire d'un rectangle 29-10-11 à 12:36

pardon j'avais pas vu le 1er commentaire merci

Posté par
Hiphigeniere : Problème: Aire d'un rectangle 29-10-11 à 22:29

OK !

Posté par
jeancmre : Problème: Aire d'un rectangle 30-10-11 à 11:51

par contre je galère un peu sur la 4...

Posté par
Hiphigeniere : Problème: Aire d'un rectangle 30-10-11 à 22:11

Pour la 4 ...

4. a. A l'aide de la définition d'une fonction décroissante montrer que la fonction u(X)= (X²-8)² est décroissante sur l'intervalle [0 ; 2√2].


La définition de décroissance pour la fonction u sur l'intervalle [0 ; 2√2] est la suivante :

Pour tous les réels x1et x2 appartenant à l'intervalle [0 ; 2√2],   x_1<x_2\Longrightarrow u(x_1)>u(x_2)

ou encore,

Pour tous les réels x1et x2 appartenant à l'intervalle [0 ; 2√2],   x_1<x_2\Longrightarrow (x_1^2-8)^2>(x_2^2-8)^2.  

En effet,

x_1, x_2 \in [0;2\sqrt{2}]\ et\ x_1<x_2\Longrightarrow 0<x_1<x_2<2\sqrt{2}

x_1, x_2 \in [0;2\sqrt{2}]\ et\ x_1<x_2\Longrightarrow 0<x_1^2<x_2^2<(2\sqrt{2})^2

x_1, x_2 \in [0;2\sqrt{2}]\ et\ x_1<x_2\Longrightarrow 0<x_1^2<x_2^2<8

x_1, x_2 \in [0;2\sqrt{2}]\ et\ x_1<x_2\Longrightarrow x_1^2-8<x_2^2-8<0

x_1, x_2 \in [0;2\sqrt{2}]\ et\ x_1<x_2\Longrightarrow (x_1^2-8)^2>(x_2^2-8)^2

Tu peux justifier les passages entre chaque ligne ?

Posté par
boubkerere : Problème: Aire d'un rectangle 30-10-11 à 22:13

pourrais je apres avoir un peu daide hiphegenie please

Posté par
Nitrate33re : Problème: Aire d'un rectangle 11-12-11 à 17:22

Comment faites-vous pour trouver le maximum svp ?

Posté par
Hiphigeniere : Problème: Aire d'un rectangle 11-12-11 à 21:42

Bonsoir Nitrate33

Tu n'as pas compris mon message de 19h08 ?

Posté par
cessmenudre : Problème: Aire d'un rectangle 22-12-11 à 15:36

Bonjour à tous ! Voilà j'ai le même exercice à faire et je n'ai pas compris comment on trouve l'ensemble de définition (question 1)... Est-ce que quelqu'un pourrait m'expliquer comment on arrive à ce résultat ? Merci d'avance ainsi que pour les explications de l'exercice en entier.

Posté par
Hiphigeniere : Problème: Aire d'un rectangle 22-12-11 à 19:15

Bonsoir

Citation :
je n'ai pas compris comment on trouve l'ensemble de définition (question 1)...
Tu détermines l'ensemble des valeurs possibles que peut prendre x.

On sait que x = ON.
Quelle est la valeur minimale de x ?
Quelle est sa valeur maximale ?

Regarde ce dessin

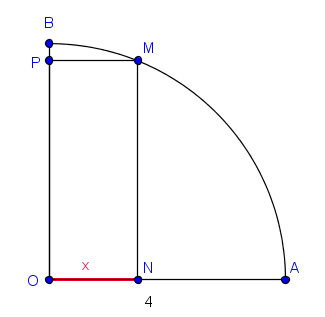
Problème: Aire d\'un rectangle

Posté par
cessmenudre : Problème: Aire d'un rectangle 22-12-11 à 19:40

Ça y est j'ai compris ! La valeur minimale est 0 et la valeur maximale est 4 d'où D=[0;4].
Merci beaucoup !

Posté par
Hiphigeniere : Problème: Aire d'un rectangle 22-12-11 à 19:44

Posté par
cessmenudre : Problème: Aire d'un rectangle 23-12-11 à 16:59

Bonsoir. Voilà cette fois ci c'est la question 3) b) que je n'ai pas compris...Puis-je avoir de l'aide ? Merci d'avance.

Posté par
Hiphigeniere : Problème: Aire d'un rectangle 23-12-11 à 17:44

Tu n'as pas compris mon message de 19h08 ?
Sinon, je peux te l'expliquer autrement

Posté par
cessmenudre : Problème: Aire d'un rectangle 26-12-11 à 21:37

Non justement je n'ai pas compris...
(Désolée de ma réponse tardive mais il y a eu Noël donc je n'ai pas eu l'occasion d'aller sur le site plus tôt.)

Posté par
Hiphigeniere : Problème: Aire d'un rectangle 26-12-11 à 22:40

Pas de problème.
J'espère que Noël à été excellent pour toi

On a ceci :

(x^2-8)^2\ge 0  (un carré n'est jamais négatif)

-(x^2-8)^2\le 0  (attention, le sens de l'inégalité change)

64-(x^2-8)^2\le 64  (en ajoutant 64 aux deux membres de l'inégalité)

\sqrt{64-(x^2-8)^2}\le \sqrt{64}  (parce que la fonction racine carrée est croissante sur R+.

f(x) \le 8  (puisque f(x)=\sqrt{64-(x^2-8)^2}).

Donc 8 est un majorant de la fonction f.

Et de plus,

f(x) = 8 \Longleftrightarrow \sqrt{64-(x^2-8)^2}=8\Longleftrightarrow 64-(x^2-8)^2=64\\\\\Longleftrightarrow -(x^2-8)^2=0\Longleftrightarrow (x^2-8)^2=0\\\\\Longleftrightarrow x^2-8=0\Longleftrightarrow x^2=8\Longleftrightarrow x=\pm \sqrt{8}\Longleftrightarrow x=\pm 2\sqrt{2}

Or x0.

Ainsi f(x) = 8\ \ si\ \ x =2\sqrt{2}.

Par conséquent, le maximum de f est 8 et ce maximum est atteint si x = 2\sqrt{2}

Posté par
cessmenudre : Problème: Aire d'un rectangle 26-12-11 à 23:01

Oui j'ai passé un excellent Noël merci

Et merci beaucoup pour ta réponse, j'ai tout compris, je n'aurai jamais réussi sans

Posté par
Hiphigeniere : Problème: Aire d'un rectangle 26-12-11 à 23:03

Posté par
cessmenudre : Problème: Aire d'un rectangle 27-12-11 à 13:59

Bonjour ! (Et oui c'est encore moi )
Je voudrai savoir si pour la question 4) b) (En déduire le sens de variation de f sur l'intervalle [0; 22].) on trouvait bien que celle-ci était croissante...ou me suis-je trompée ?
Merci d'avance

Posté par
Hiphigeniere : Problème: Aire d'un rectangle 27-12-11 à 21:24

Oui, la fonction f est bien croissante sur cet intervalle.  

Posté par
cessmenudre : Problème: Aire d'un rectangle 27-12-11 à 21:34

Ah yes ! Merci

Et pour la 4) d) je ne sais pas comment faire. Pourrais-je avoir une petite indication ?

Posté par
cessmenudre : Problème: Aire d'un rectangle 27-12-11 à 21:38

Non pas la d) ! La c) ! Pardon.

Posté par
Hiphigeniere : Problème: Aire d'un rectangle 27-12-11 à 21:57

Tu reprends les questions 4a) et 4b)

Citation :
4. a. A l'aide de la définition d'une fonction décroissante montrer que la fonction u(X)= (X²-8)² est décroissante sur l'intervalle [0 ; 2√2].
   b. En déduire le sens de variation de f sur [0 ; 2√2].
et tu démontres ceci :

*) a) A l'aide de la définition d'une fonction croissante montrer que la fonction u(X)= (X²-8)² est croissante sur l'intervalle [2√2;4].
*)  b. En déduire le sens de variation de f sur [2√2;4].

Posté par
cessmenudre : Problème: Aire d'un rectangle 27-12-11 à 22:15

Mais je refais pareil que les questions a) et b)? Je dois changer des choses quand même non ?

Posté par
Hiphigeniere : Problème: Aire d'un rectangle 27-12-11 à 22:17

Evidemment que tu dois changer des choses...
Réfléchis un peu !  

Posté par
cessmenudre : Problème: Aire d'un rectangle 28-12-11 à 19:20

Pourquoi j'ai fait S ?....je comprends rien...

Posté par
Hiphigeniere : Problème: Aire d'un rectangle 28-12-11 à 19:33

Et moi, je ne comprends pas ton dernier message...

Posté par
cessmenudre : Problème: Aire d'un rectangle 28-12-11 à 19:41

Je suis en première S et comme là je comprends pas comment faire bah je me demande pourquoi j'y suis en première S comme je n'y arrive pas...

Posté par
Hiphigeniere : Problème: Aire d'un rectangle 28-12-11 à 22:15

A 22h11, j'ai écrit en toutes lettres la définition de la décroissance de la fonction u.

Pour le problème que tu soulèves, il s'agit de la croissance.
Tu dois être capable de citer cette définition !

Posté par
cessmenudre : Problème: Aire d'un rectangle 28-12-11 à 22:41

Oui oui je la connais la définition. Mais ce que je comprends pas c'est s'il faut faire la même chose que la question a) ou s'il faut faire autrement ? Parce que je vois pas comment arriver à une fonction croissante...
Désolée de vous embêter avec tout ça.

Posté par
Hiphigeniere : Problème: Aire d'un rectangle 28-12-11 à 22:48

A priori, on ne sait pas si la fonction est croissante ou décroissante sur [2\sqrt{2},4].

On ne le sait qu'à la fin de l'explication.

Tu reprends mon message de 22h11 comme référence et tu commences comme ceci :

x_1, x_2 \in [2\sqrt{2},4]\ et\ x_1<x_2\Longrightarrow ...

A toi de remplir les points de suspension et de continuer comme dans le post en question.

Posté par
cessmenudre : Problème: Aire d'un rectangle 29-12-11 à 12:40

Bonjour, j'ai bien repris ta méthode mais...je la trouve décroissante. C'est pas normal...

Posté par
cessmenudre : Problème: Aire d'un rectangle 29-12-11 à 13:55

Cette question me bloque pour finir mon devoir...ça m'énerve

Posté par
Hiphigeniere : Problème: Aire d'un rectangle 29-12-11 à 18:48

Alors, une chose à la fois...

Qu'as-tu écrit pour terminer cette ligne ?
x_1, x_2 \in [2\sqrt{2},4]\ et\ x_1<x_2\Longrightarrow ...

Posté par
cessmenudre : Problème: Aire d'un rectangle 29-12-11 à 19:14

Moi j'ai l'habitude de prendre x et y donc ça fait:
22 < x < y < 4
8 < x² < y² < 16
0 < x²-8 < y²-8 < 8
0 > (x²-8)² > (y²-8)² > 64

Posté par
Hiphigeniere : Problème: Aire d'un rectangle 29-12-11 à 19:22

Pourquoi changes-tu le sens des inégalités à la dernière ligne ?

Posté par
cessmenudre : Problème: Aire d'un rectangle 29-12-11 à 19:28

C'est ce que vous aviez fait dans le message de 22h11...

Posté par
Hiphigeniere : Problème: Aire d'un rectangle 29-12-11 à 19:39

Oui, mais dans le message de 22h11, à la ligne qui précédait, nous avions une inégalité entre deux valeurs négatives !

Tu en comprends l'importance ?

Posté par
cessmenudre : Problème: Aire d'un rectangle 29-12-11 à 20:11

Non je ne comprends pas...

Posté par
Hiphigeniere : Problème: Aire d'un rectangle 29-12-11 à 21:36

Je vais te donner deux exemples.

Si a et b sont positifs, alors a<b\Longrightarrow a^2<b^2

Exemple :

3<5\Longrightarrow 3^2 \red{<} 5^2

3<5\Longrightarrow 9<25

Si a et b sont négatifs, alors a<b\Longrightarrow a^2>b^2

Exemple :

-6<-3\Longrightarrow (-6)^2 \red{>} (-3)^2

-6<-3\Longrightarrow 36>9

Posté par
cessmenudre : Problème: Aire d'un rectangle 29-12-11 à 22:41

Ah d'accord ! Ca y est j'ai compris !
Merci beaucoup pour tes explications
Je vais enfin pouvoir terminer ce devoir. Encore un grand merci à toi !

Posté par
Hiphigeniere : Problème: Aire d'un rectangle 29-12-11 à 22:45

Tu as donc compris que dans ce cas-ci, les inégalités conservent le même sens.

0 < x²-8 < y²-8
0 < (x²-8)² < (y²-8)²

Tu peux donc conclure...

Bonne soirée

Posté par
Lady56re : Problème: Aire d'un rectangle 31-12-11 à 15:17

Bonjour j'ai moi aussi à faire cette exercice , j'ai voulu me corriger pour certaine choses qui se sont révélées bonne .
La seule chose que je ne comprend pas c'est pour la question 4.b , pour moi le sens de variation de f sur l'intervalle [o;2racine de 2] était décroissant et non croissant .
Pouvez vous m'expliquer ?

1 2 3 +


Rechercher
Menu
Espace membre
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1674 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !