Inscription / Connexion Nouveau Sujet
la courbe de Béziers
Bonjour
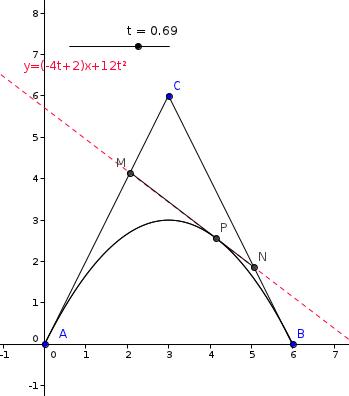
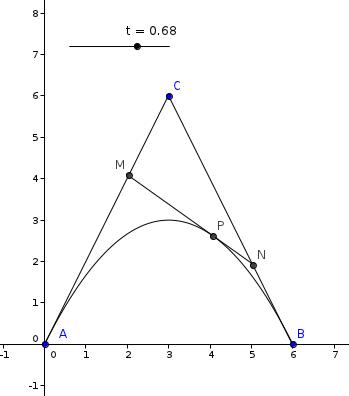
On a un réel t de [0;1] et des points M,N,P tels que vecteur AM = t*vecteur AC, vecteur CN=t*vecteur CB, vecteur MP= t* vecteurMN
j'ai fait la figure et maintenant on me demande d'exprimer en fonction de t les coordonnées de M, N, P j'aurai besoin d'aide s'il vous plait
oui, tu avais oublié de le dire...
passage aux coordonnées
application numérique
résolution
simplification
je ne sais pas ce chapitre nous l'avons fini depuis longtemps je ne sais pas pour quoi j'ai oublié la formule
tu le fais exprès ou tu as vraiment un problème ?
tu as oublié de nous communiquer de quelles conjectures il était question.
ah, ça va mieux en le disant, hein ?
mais tu n'as pas tout dit, c'est incroyable (même si je peux deviner ce que tu omets, il serait urgent que tu t'améliores à ce sujet) : quelle parabole ?
que sais-tu des tangentes à une courbe ?
soit f une fonction dérivable en un point , de nombre dérivé
en ce point, alors une équation de sa tangente est :
il te reste à montrer que les droites (AC), (BC), (MN) sont effectivement des tangentes à cette fantomatique parabole, et donner les points de contact de ces tangentes.
le problème c'est que en cours nous n'avons jamais appliquée cette formule nous l'avons juste écrite
ah, si tu n'as pas déjà vu le corrigé de cet exercice, tu ne peux pas le résoudre, c'est clair.
Mais tu ne m'as toujours pas dit comment ton exercice introduit cette parabole. Elle sort d'où ?

En fonction du paramètre , le point P a pour coordonnées
ce point P a des coordonnées , et si on pose
, alors
cette parabole porte l'ensemble des points P obtenus lorsque varie de 0 à 1
on étudie la fonction
en particulier sa fonction dérivée est
la tangente en A a pour équation
or tu montreras que la droite (AC) a pour équation
la tangente en B a pour équation
or tu montreras que la droite (AC) a pour équation
Soit alors P le point de coordonnées
la tangente en P à cette parabole a pour équation
avec d'ailleurs ,on retrouve le fait que P est sur cette parabole.
or tu montreras que la droite (MN) a pour équation