Inscription / Connexion Nouveau Sujet
Equations
Coucou ^^ voila j'ai des exercices de maths à faire sur des équations et autres, j'espere que vous m'aiderez et que j'arriverai à comprendre grace a ca ^^
Ex partie A : Pour determiner une solution positive d'équations du type x2 (le 2 c'est la puissance) + bx = c où b et c sont deux nombres positifs. Al Khwarismi utilise une méthode à support géométrique.
Par ex : pour l'équation x2 + 10x = 96, il propose de tracé un carré de coté x et de compléter par deux rectangles de dimensions x et la moitié de 10 pour obtenir un grand carré.
Ce grand carré a pour aire (x2 + 10x) + 52 ( 2 est la puissance donc 5 puissance 2)
c'est a dire 96 + 25 = 121
Donc il a pour coté 11. Il suffit de retirer 5 pour obtenir le coté x cherché :
x = 6
Resoudre en utilisant cette méthode les équations suivantes (on fera dans chaque cas un croquis)
a) x2 ( x puissance 2) + 12x = 45
b) x2 ( x puissance 2) +2x = 8
c) x2 ( x puissance 2) + 20x = 21
Voici une traduction de la méthode par un programme de calcul pour l'équations x2 ( x puissance 2) + 10x = 96
. Diviser 10 par 2
. Elever ce quotient au carré
. Additionner ce carré à 96
. Prendre la racine carré de cette somme
. Retrancher à ce resultat le quotient du début
1) a. Prouver que l'équation x2 + 10x = 96 équivaut à (x + 5) au carré = 121
b. Résoudre cette équation.
c. Verifier que le programme de calcul donne bien une solution positive de cette l'équation.
2) Trouver en utilisant la méthode de programme de calcul une solution positive de l'équation:
x2 + 8x = 2009
3) En admettant que cette methode donne la seule solution positive pour les equations de type x2 + bx = c où b et c sont deux nombres positifs, écrire un algorithme en langage codé qui demande les valeurs de a et de b et affiche la solution positive de l'équation.
Partie B
On considere la fonction f definie par R par : f(x) = (x+3) au carré - 4. On designe par (C) sa courbe representative dans un repere du plan.
1) Developper et factoriser
2) Determiner les coordonnées du point d'intersection de (C) avec l'axe (Oy)
3) Determiner les coordonnées du point d'intersection de (C) avec l'axe (Ox)
4) Determiner les coordonnées du point d'intersection de (C) dont l'ordonnée est égale à 5.
Voila j'espere que vous m'aiderez un peu parce que j'ai vraiment rien compris :s
Merci d'avance 
Bonjour
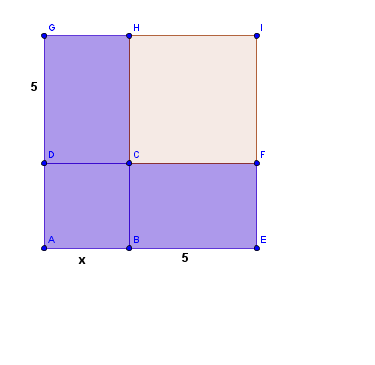
voilà un dessin pour expliquer la partie A
en bleu, une aire qui représente le membre de gauche de ton équation
x²+5x+5x soit x²+10x
le carré rose a une aire de 5.5 soit 25
(x²+10x)+25 fait donc 96+25 puisqu'on te dit au départ que x²+10x doit être égal à 96
donc en tout j'ai 121 qui représente l'aire du grand carré
121 est le carré de 11
donc un côté mesure 11
mais 11, c'est 6 de plus que 5
donc x=6 est une solution du problème
dans la parie A, on te demande de refaire ça avec les autres équations
j'espère que cet exemple va t'y aider!...