Inscription / Connexion Nouveau Sujet
Calcul d'arête dans une pyramide
Bonjour,
Je cherche à calculer la longueur de la 4e arête d'une pyramide à base rectangulaire, connaissant la longueur des 3 autres.
J'ai essayé avec le théorème de Thalès mais ça ne me paraît pas possible.
Auriez-vous une idée d'une méthode appropriée ?
Bien cordialement,
édit Océane : forum modifié
je n'ai un angle droit que dans la base qui est un rectangle, je ne vois pas comment je pourrais l'utiliser pour le calcul des arêtes ?
En fait ton problème n'est pas bien défini.
Est ce que tu connais les côtés du rectangles ?
De façon générale, il faut utiliser la projection orthogonale du sommet de la pyramide sur la base.
Bonjour.
Soit P le pied de la hauteur dans la base rectangulaire ABCD.
Il est facile de démontrer que PA²+PC² = PB²+PD².
En ajoutant à chacun de ses termes le carré de la hauteur, on trouve que la somme des carrés de deux arêtes opposées est égale à la somme des carrés des deux autres arêtes.
Trois solutions selon l'arête opposée à l'arête inconnue.
Bonsoir,
à défaut de calcul, une construction géométrique de la 4ème arète SD = d, d'une pyramide à base rectangulaire de dimensions u et v (qui doivent bien entendu être connues, sinon le pb est insoluble = indéterminé), et connaissant les 3 arètes SA = a, SB = b, SC = c
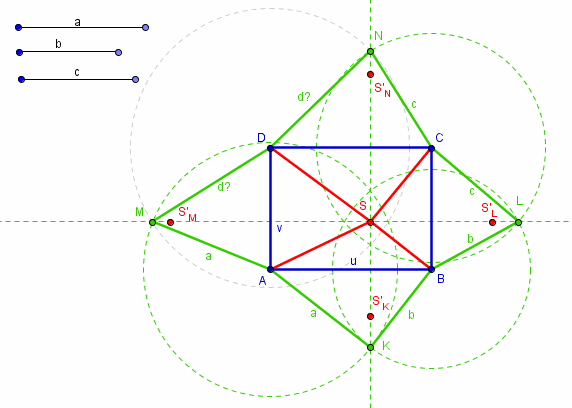
Cette construction construit le patron (en vert) et la projection orthogonale (en rouge) sur la base.
Le patron donne les faces en vraie grandeur, donc la mesure en vraie grandeur de l'arête inconnue d.
La pyramide n'est réelle que si les triangles "en projection" sont plus petits que les triangles en vraie grandeur (d'où les "points de test" S'K etc)
La construction n'est pas détaillée, mais assez intuitive et évidente.
On devrait pouvoir transformer cette construction en calcul ...
Bien vu, plumemeteore
et cela montre que même si on ne sait pas construire la pyramide, cette 4ème arête est calculable sans connaitre les dimensions u et v !
(qui sont bien indéterminées, mais on ne les demande pas de toute façon ...)
Bonjour
Comme mathafou je te conseille un "patron"
tournant
Soit le rectangle ABCD et le sommet S
tu connais AB =CD et BC=DA
et aussi AS BS et CS
donc trace ASB et SBC un cercle de centre C et de rayon CD
et un cercle de centre S et de rayon AD.
le point D sera à l'intersection de ces deux cercles et donc
tu auras facilement la distance DS qui est le 4 ème coté
Bonjour dpi,
tu connais AB =CD et BC=DA
donc non, on ne connait pas
C'est en cela que réside la beauté de la solution de plummeteore : on n'a pas besoin de connaitre la base pour calculer la 4ème arète !!
ce théorème faisait l'objet d'un DM très récent sur ![]() Géométrie plane..
Géométrie plane..


