Inscription / Connexion Nouveau Sujet
position d une courbe par rapport à sa tangente
Soit f la fonction carré et P la parabole la représentant
a. Calculer f'(a) .Déterminer sous la forme y=mx+p une équation de la droite D tangente à P au point d'abscisse a.
b. Montrer que tous les points de P sont au-dessus de D, c'est-à-dire que la différence f(x)-(mx+p) est toujours positive.
Soit g la fonction racine carrée et C sa courbe représentative.
c. Calculer g'(a) .Déterminer sous la forme y=mx+p l'équation de la droite ^ , tangente à C au point d'abscisse a.
d. Montrer que tous les points de C sont au-dessus de ^ .
Soit la fonction h définie sur i par : h(x)=x^3-2x+1 et < sa courbe représentative.
e. Calculer h'(o) .Déterminer une équation de la tangente (T ) à < au point d'abscisse 0.Ce résultat était-il prévisible ?
f. Observer (T ) et < sur l'écran d'une calculatrice graphique. Quelle conjecture peut-on faire concernant leurs positions relatives ? Prouver ce résultat.
g. Déterminer une équation de la tangente (T ) à < au point d'abscisse a. Montrer que, si a est positif, tous les points de < d'abscisse positive sont au-dessus de (T ) et que, si a est négatif, tous les points de < d'abscisse négative sont au-dessous de (T)
j'ai réussi a tout faire plus ou moins il y a juste la question f où je coince, vous pouvez m'aider svp
merci
bonsoir
c'est quoi "<" ? une nouvelle lettre ? c'est rare pour une courbe
la position relative c'est dire laquelle est au-dessus de l'autre sur les differents intervalles donc tu regardes ta calculatrice et tu dis si la tangente est sur ou sous la courbe
salut arno
pour les positions de la tangente par rapport a la parabole tu prends l"equation de la tangente T(x)=F"(x[/sub]0)(X-x[sub]0)+F(x[sub][/sub]0) TU LA SOUSTRAIS A celle de la parabole puis tu observe le signe de la differance
Soit f la fonction carré et P la parabole la représentant
a. Calculer f'(a) .Déterminer sous la forme y=mx+p une équation de la droite D tangente à P au point d'abscisse a.
b. Montrer que tous les points de P sont au-dessus de D, c'est-à-dire que la différence f(x)-(mx+p) est toujours positive.
Soit g la fonction racine carrée et C sa courbe représentative.
c. Calculer g'(a) .Déterminer sous la forme y=mx+p l'équation de la droite T , tangente à C au point d'abscisse a.
d. Montrer que tous les points de C sont au-dessus de T .
Soit la fonction h définie sur i par : h(x)=x^3-2x+1 et C sa courbe représentative.
e. Calculer h'(o) .Déterminer une équation de la tangente (T ) à C au point d'abscisse 0.Ce résultat était-il prévisible ?
f. Observer (T ) et C sur l'écran d'une calculatrice graphique. Quelle conjecture peut-on faire concernant leurs positions relatives ? Prouver ce résultat.
g. Déterminer une équation de la tangente (T ) à C au point d'abscisse a. Montrer que, si a est positif, tous les points de C d'abscisse positive sont au-dessus de (T ) et que, si a est négatif, tous les points de C d'abscisse négative sont au-dessous de (T)
donc voila j'ai corriger le sujet
je dit bien qu'il n'y a que la f) que je n'arrive pas, le reste c'est bon
bonjour! en faite mon prof ma donner un dm à faire et je suis ne comprend rien pourriez vous maider :
exo 1
dans le repère (o, i , j), on considere la parabole P d'équation y = [sub]x et la droite D d'équation y= -2x-1.
1°) déterminez le ou les points communs à P et D.
cette question jarrive a faire mais apre non
2°) à l'aide de la figure
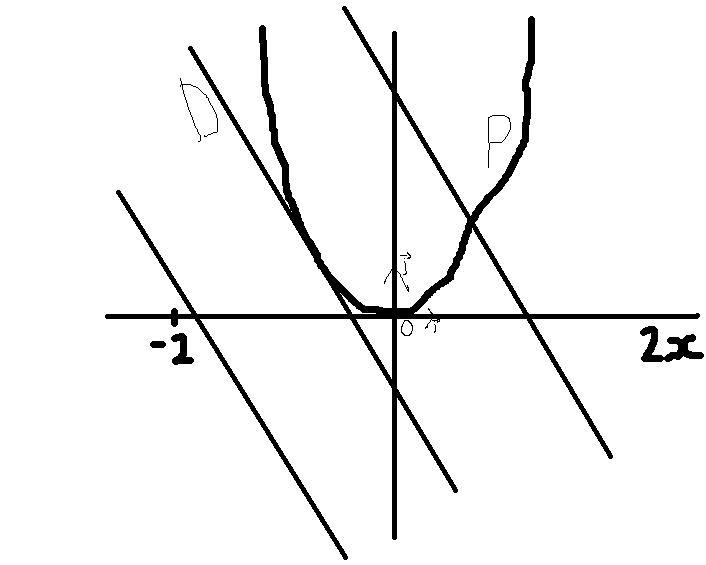
POSITION D'UNE DROITE PAR RAPPORT A UNE PARABOLE
Dans le repère (O, ⎯→i, ⎯→j), on considère la parabole P d'équation y = x2 et la droite D d'équation y = - 2x - 1.
1.
a) Déterminer les coordonnées du point commun à P et D. b) A l'aide de la figure ci-dessus, donner l'équation réduite d'une droite D', parallèle à D et n'ayant aucun point commun avec P. Vérifier algébriquement.
2.
On considère maintenant les droites d'équation : y = 3x + p, où p est un réel quelconque. a) Indiquer une propriété commune à toutes ces droites. Visualisation graphique : Menu Graphe
stat edit et en liste L1 entrer les entiers de -3 et 3
y= X[sup][/sup]2 et Y =3X+L1
b) Déterminer p pour que la droite correspondante ait un seul point commun avec P.
On dit que la droite obtenue est tangente à P.


