salut
toutes les aretes mesurent a signifie les cotes du carre ainsi que les cotes lateraux de la pyramide
tu peux considerer le triangle rectangle en O OSA
tel que O centre du carre et pied de la hauteur abaissee de S(car la pyramide est reguliere)
tu appliques pythagore sachant que hypotenuse=SA=a
et AO=(aV2)/2

merci beaucoup
je vois que j'avais cherché à faire trop compliqué

kel è la formule pr calculer la hauteur d'une pyramide a base rectangulaire?? mci d'avance!

Salut !
j'aimerai savoir kel è la formule pr calculer la hauteur d'une pyramide a base rectangulaire. Mci d'avance!

Tout ne se résume pas à des formules, il faut réfléchir.



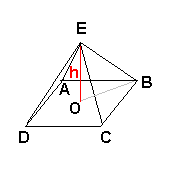
Soit "a" la longueur d'une arète de la pyramide.

DB = a.V2   (Avec V pour racine carrée).
OB = (1/2).DB = a/V2

Dans le triangle EOB rectangle en O: Pythagore:

EB² = OE² + OB²

a² = h² + (a/V2)²
a² = h² = (a²/2)
h² = a²/2

h = a/V2
-----
Vérifie.  

    Bonjour Kro. Tu n'as pas lu les consignes données aux posteurs ?... Alors fais -le, et ne poste pas de nouvelle question dans un topic lancé par Morwenn.
    Et ensuite, tu nous indiqueras tes données, les différentes mesures, ce que tu as fait, etc.   Au travail !   J-L

Slt!
Aidez moi, j'ai un devoir commun pour Lundi et voici l'énoncé :


On considère une pyramide régulière SABCD à base carrée ABCD dont toutes les arêtes mesurent a=4cm.
Calculer la valeur exacte de la hauteur h de cette pyramide et en déduire son volume.

Voila j'ai tout oubliée depuis la 4ème, donc soyez sympa

Pardon j'ai oubliée aussi :
En déduire son volume.

Et pour cela j'ai fait
V² = 1/2 X 16 X 5,5
V² = 29.3

(Pour info j'ai trouvé 5,5cm la hauteur)
Donc 29.3 pour le volume, est t-il bon??

Merci de votre aide!

Dans mon message du 09/08/2006 à 11:34, j'ai montré que h = a/V2

donc: h = 4V2 cm (avec V pour racine carrée).
-----
Et V = (1/3) Aire de la base carrée * hauteur

V = (1/3) * 4² * 4V2

V = (64V2)/3 cm³
-----
Sauf distraction.  

DOnc la réponse a mon exo est V = (64V2)/3 cm³ ?
/Merci beaucoup!

bonjour jai besoin d'aide pour ojourd'huit si possible alors il faut me trouver deux pyramide pas forcément de meme base mais qui doivent avoir le meme volume tout les deux ce res possible d'avoir les patron de ses pyramide merci d'avence

    Bonjour Marie-Ch...   Deux pyramides qui ont même volume :  le plus simple, même base, et même hauteur !...

Je n'ai pas compris pourquoi AO=(a/V2)²

    Bonjour . Et toi, tu as trouvé combien pour  AO ?

Relis donc le message qui donnait AO ...