mesurer des angles

Posté par stany (invité)

Bonjour à tout le monde.

J'ai tenté de résoudre l'exercice ci-joint mais je ne sais plus comment mesurer des angles. Pouvez-vous m'aider à me donner une méthode ?

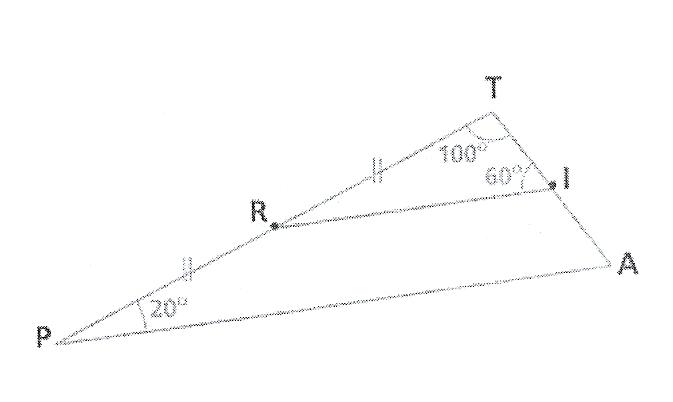
1) calculer la mesure de l'angle TRI (voir la figure pour les données).
2) Que peut-on dire des angles TRI et RPA ?
3) Montrer que I est le milieu de [TA]

Merci
Stany

Posté par infophile infophile

Bonjour

Que sais-tu sur la somme des angles d'un triangle ?

Posté par stany (invité)

Pouvez-vous m'indiquer une formule sur la somme d'un triangle ?

Si je vous demande une aide c'est que je ne connais pas la formule pour pouvoir calculer ces mesures.

Merci;

Posté par infophile infophile

Ok.

La somme des angles d'un triangle est égale à 180°

Posté par stany (invité)

Merci du coup de pouce mais cela m'éclaire pas plus.

1) Si je comprends bien l'angle TRI est égal à 180° ?
2) Je ne vois ce qu'il faut dire ou démontrer ?
3) Quel est le théorème à utiliser pour démontrer ?

Pouvez-vous me donner davantage d'éléments ?

Merci

:?

Posté par plumemeteore plumemeteore

bonjour Stany
l'angle TRI n'est pas égal à 180°; c'est la somme de cet angle et de ses deux compagnons dans le triangle TRI qui est égale à 180 degrés
remarque ensuite que les angles TRI et RPÄ sont des correspondants (sécante TP, droites RI et PA) donc...

Posté par stany (invité)

Merci. Mais je ne comprends rien (désolé pour ma grande faiblesse en maths).

Comment calculer l'angle TRI ? Pouvez-vous me donner un exemple pour mieux comprendre.

1) L'angle TRI est-il alors = à 160° (180 - 20) ???

2) les angles TRI et RPA sont donc correspondants. Qu'est-ce que cela veut dire ? Comment le montrer avec quel théorème ?

Pouvez-vous svp me donner un exemple pour résoudre cet exercice avec des explications. Je ne fais exprès de rien comprendre.
  
Merci encore pour l'aide

Posté par Nicolas_75 Nicolas_75

Bonjour stany,

Il faudrait réfléchir plus à ce que tu écris.
TRI = 160° ?
Cela veut dire que TRI est presque un angle plat (180°) : ce n'est clairement pas le cas sur la figure.

La somme des angles du triangle TRI vaut 180°
Donc : 100° + 60° + TRI = 180°
Donc TRI = ???

Nicolas

Posté par stany (invité)

Merci Nicolas. J'ai enfin compris un peu mieux les choses. Pouvez-vous encore m'aider.

1) TRI = 180° - 100° - 60°
   TRI = 20°

2)Que peut-on dire des angles TRI et RPA ?

Je ne comprends pas cette question. Pouvez-vous m'aider ?

3) Montrer que I est le milieu de [TA]

Est-ce juste :

Dans le triangle PTA :
on sait que :

R est milieu du côté [PT]
La droite (RI) est parallèle à la droite (PA)

Or dans un triangle, la droite passant par le milieu d'un côté et parallèle à un second côté coupe le troisième côté en son milieu donc : I est le milieu du côté [TA].  

MERCI

Posté par Nicolas_75 Nicolas_75



Oui !!!

Reste à montrer pourquoi (RI) est parallèle à (PA)

Posté par Nicolas_75 Nicolas_75

Pour 2) et pour montrer que (RI) est parallèle à (PA), ceci devrait t'aider :
http://homeomath.imingo.net/anglepar.htm

Posté par stany (invité)

Comment résoudre cette question :

2°) que peut-on dire des angles TRI et RPA ?

Que doit-on démontrer ?

Posté par Nicolas_75 Nicolas_75

Tu as montré que TRI = 20°
L'énoncé dit que RPA = 20°
Donc TRI = RPA (= 20°)
Donc (RI)//(PA)
Donc, comme R est le milieu de [TP], I est le milieu de [TA] (propriété de la droite des milieux)

Posté par stany (invité)

Merci pour votre aide. Je connais la propriété de la droite des milieux mais j'étais incapable de l'appliquer.

A bientôt
Stany

Posté par Nicolas_75 Nicolas_75

Je t'en prie.