Ne peux-tu commencer par les premières questions ?

Et bien, il y a déjà une figure pour la deuxième question (je pense que la première question ne devrait vraiment pas poser problème)

Cordialement.

je ne comprends pas.
tu te sens capable de nous transmettre ton exercice par mail, mais tu peux aussi nous fournir la figure sur ce site et recopier les questions.

En fait, les règles du forum n'encouragent pas les communications privées.

Je croyais qu'on ne pouvais pas scanner  =/

pas de document complet
tu recopies l'énoncé et tu fournis la partie du graphique qui y est associée.

Que le grand cric me croque si j'ai mal interprété les règles du forum. J'implore dans ce cas l'immense mansuétude des modérateurs.

Trés bien  
J'enverrai cela en fin d'après midi car la je dois m'absenter
Merci d'avance

Cordialement

Cindy  

Voici l'énoncé:

f est la fonction x ==> x² restreinte à l'intervalle [0;1] et P sa courbe dans un repère orthonormal. Pour tout entier n, n >(strictement)2, on partage l'intervalle [0,1] en n sous-intervalles de même longueur.

1. Cas n = 5

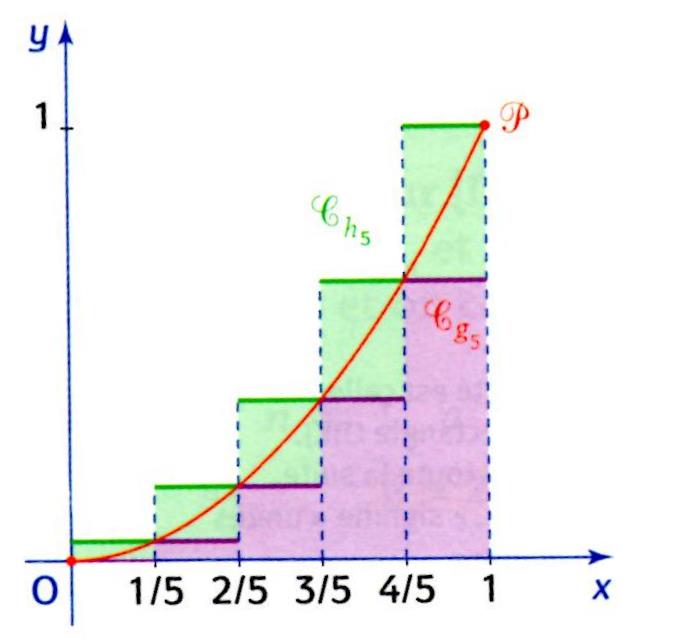
Sur la figure ci-joint, les fonctions en escalier sont représentées en rouge et en vert. Il est clair que g5 <(strictement) f <(strictement) h5 sur [0;1].

a) Aucune difficulté pour cette question  

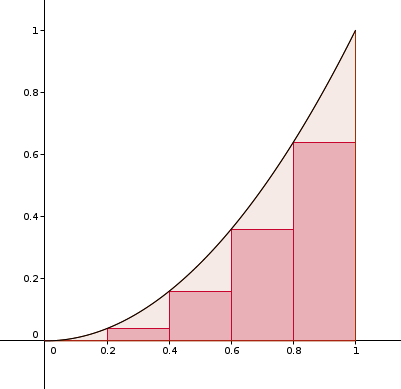
b) L'unité d'aire étant celle du carré de côté 1, indiquez sur la figure l'aire associée à I(g5), celle associée à I(h5) puis celle associée ) la différence I(h5) - I(g5).
Ainsi "l'aire sous la parabole" P est encadrée par I(g5) et I(h5).

2. Cas général

On suppose n quelconque, n >(strictement) 2, et on pose sn = 1/n [f(0) + f(1/n) + ... + f(n-1 /n)].
Comme dans le cas n = 5, sn est la somme des aires des rectangles inférieurs, donc sn est l'intégrale d'une fonction en escalier définie par:

gn(x) = (k/n)² si x est dans l'intervalle ]k/n , k+1 /n[ avec 0 <(strictement) k <(strictement) n - 1.

De même, on pose Sn = 1/n [f(1/n) + f(2/n) + .... + f(n/n)]; Sn est la somme des aires des rectangles supérieurs, donc Sn est l'intégrale de la fonction en escalier hn définie par:

hn(x) = (k+1 / n)² si x est dans l'intervalle ]k/n , k+1 /n[ avec 0 <(strictement) k <(strictement) n - 1.


Questions:

a) Prouver que sn = 1/n^3 [1² + 2² + .... (n-1)²] et Sn = 1/n^3 [1² + 2² + .... n²]

b) Exprimer sn et Sn en fonction de n. Démontrez que (sn) est une suite croissante et (Sn) une suite décroissante.

c) Calculez Sn - sn en fonction de n puis prouvez que lim (Sn - sn) = 0 quand n tend vers  l'infini.
Justifiez que les suites (sn) et (Sn) convergent vers un réel que vous préciserez.



Voici l'énoncé au complet. Comme vous pouvez le voir, beaucoup d'énoncé et peu de questions
J'espère que vous saurez m'aider.  
En tout cas, pour chaque réponse donné ou tout autres indications, je m'engage à tout refaire par la suite de mon coté     

Cet exercice est en même temps extrêmement classique, fondamental et simpliste.

Il doit te faire comprendre comment un mathématicien du nom de Riemann a fait pour généraliser la notion d'aire à celle de toute surface contenue dans des "lignes" suffisamment continues.

On sait calculer l' "aire" d'un rectangle, comme la hauteur que multiplie la base.

On découpe alors la surface à "mesurer" en rectangles de plus en plus fins, et on montre que la somme de ces rectangles, de plus en plus nombreux, mais de plus en plus petits, tend vers une limite qu'on appelle alors l' "aire" de la surface.

Ici, on a une fonction croissante sur l'intervalle [0;1] et on veut effectuer le travail de découpage sur deux familles de rectangles, les uns qui sont inclus dans la surface à mesurer, les autres qui "débordent".

est la somme des aires des rectangles quand on divise le segment [0;1] en n bandes, toutes de même largeur, (ce qui simplifie ton travail, mais est une facilité que la théorie a dû effacer), cette largeur est

Les rectangles sont numérotés, de 0 pour celui le plus à gauche, à n-1 pour celui le plus à droite, ce qui fait effectivement n rectangles.

le rectangle rouge n° k a une hauteur qui est le carré (puisqu'on étudie la fonction y=x²) de son abscisse de gauche. Cette abscisse de gauche vaut

donc ce rectangle a pour hauteur , et pour surface

La surface de tous les rectangles rouges est la somme des surfaces des n rectangles, chacun ayant une abscisse , avec k variant de 0 à (n-1)

c'est pourquoi


D'où la formule que tu as indiquée, après factorisation du terme constant

A toi de trouver une autre expression de la somme et de faire aussi la même chose pour

est ce que vous pouvez m'aider car je bloque de trop a ce dm la merci

je ne comprends pas ce que tu attends. La résolution complète ?

en faite je sais pas comment partir cette exercice la et trop compliquer pour moi si tu peux m'aider sa serait avec grande joie

S'il est trop compliqué, laisse tomber, et fais des choses moins compliquées.

Si tu veux tout de même insister, relis mes explications précédentes, je trouve que c'est un bon début pour obtenir de l'aide.

deja je sais pas quoi faire a la question 1a qui est verifiez que I(g5) = s5 et que I(h5) = S5
Je ne sais pas comment on fait pour partir

Cyndy a retranscrit un énoncé de manière partielle, ou le tien diffère du sien, mais elle ne définit pas ce qu'est s5, ni S5
Peut-être est-ce sa remarque
a) Aucune difficulté pour cette question
qui cache cette définition.
si toi, tu trouves des difficultés à la question, il va déjà falloir que tu précises l'énoncé.

Mais je te demande auparavant si tu as déjà une petite idée du but de l'exercice ?

le but est d'expliquer comment on définit l'intégrale d'une fonction continue a partir d'intégrales de fonctions en escalier je pense mais je sais absolument pas quoi faire dans cette exercice la car il me bloque et
s5= 1/5*[f(0)+f(1/5)+f(2/5)+f(3/5)+f(4/5)] et
S5 =1/5*[f(1/5)+f(2/5)+f(3/5)+f(4/5)+f(5/5)]
voila a cause de sa moi je bloque et je sais absolument pas quoi faire j'ai trop besoin de votre aide s'il vous plait monsieur

La notion d'intégrale vient de la volonté de donner une consistance à la notion d'aire pour des surfaces qui ne sont pas constituées de rectangles.

La surface d'un rectangle, c'est assez intuitif, c'est sa base que multiplie sa hauteur.

Mais la surface rose que je dessine ici :

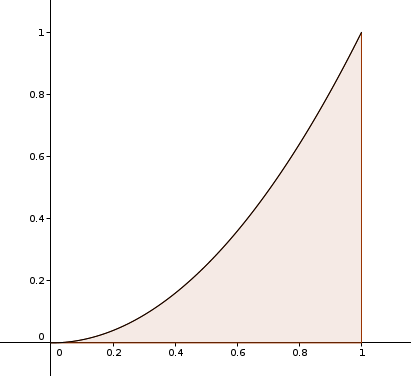
elle n'est pas constituée de rectangles.

Alors l'idée est de découper des rectangles qui vont être très proches de la "surface" à mesurer.
Et la première idée (due au Mathématicien Riemann), est de découper le segment de base en petits intervalles qui servent alors de base à ces rectangles qui vont paver la surface rose.
Après, on fait la somme des aires de tous ces rectangles pour obtenir une valeur "approchée" de l'aire rose.

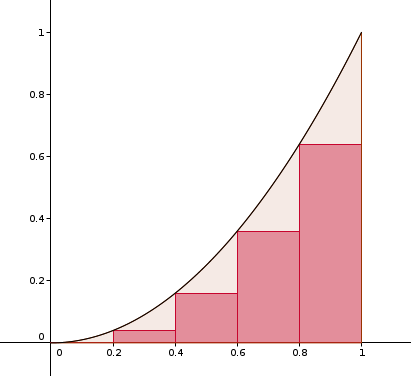
Là, la somme des aires des rectangles foncés sera inférieure à celle de l'aire rose

On peut aussi faire "dépasser" ces rectangles

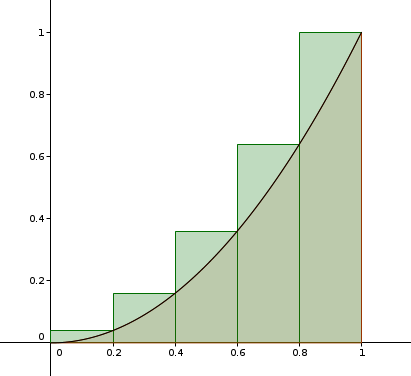
et là, on aura au contraire une somme des aires des rectangles verts qui sera supérieure à l'aire rose.

On aura un encadrement de l'aire cherchée.

mais comment veux tu que je fasse pour répondre a la question 1a et 1b sa ma aider ce que tu as fait mais je vois pas du tout comment je pourrai repondre a ces questions la

Bonjour dhalte

Je signale que sous la pression de geogeo2109 je me suis lancée dans le début de cette histoire que cindy avait débutée plus loin... Ici: https://www.ilemaths.net/sujet-aire-sous-la-parabole-et-integrale-416926.html
On a donc intérêt à regarder ce que nous faisons pour éviter trop de doublons!

la lecture de mes explications t'a pris moins de 2 minutes. je comprends que tu ne voies pas ce qu'elles pourraient d'apporter.

donc j'en reviens à ma question initiale :

j'attends un petit coup de pouce mais avec de l'explication pas la réponse directe quoi je veux aussi chercher mais je ne comprend pas tout

Ok, Camélia

mais je ne fais pas l'effort de vérifier à chaque demande si c'est un doublon.

Je fais confiance aux modérateurs pour éviter ces pratiques.

Et pour tout te dire, je ne suis pas dupe de l'objectif de georgeo, tu remarqueras peut-être que ma démarche tend à cerner si oui ou non il est prêt à réfléchir.

Tu veux mon avis ?

je suis prêt a réflechir seulement je ne comprend pas ce que veule signifier les questions poser c'est tout simple je comprend pas les questions

est ce que quelqu'un pourrait m'aider please

ok, je te prends au mot;
aide et pas résolution;
mais tu as intérêt à te bouger les méninges



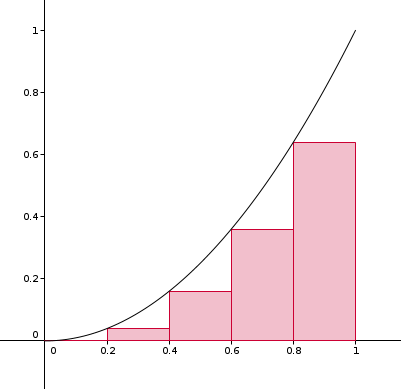
quelle est la largeur de chacun des rectangles ?

quelle est la hauteur du premier rectangle ?

quelle est la hauteur du deuxième rectangle ?

quelle est la hauteur du troisième rectangle ?

quelle est la hauteur du quatrième rectangle ?

quelle est la hauteur du cinquième rectangle ?

la largeur est de 1/5 a chaque fois
la hauteur du 1er rectangle est (1/5)²
la hauteur du 2eme rectangle est (2/5)²
la hauteur du 3e rectangle est (3/5)²
la hauteur du 4eme rectangle est (4/5)²
la hauteur du 5eme rectangle est (5/5)² soit =1
je pense que c'est sa???

pas mal, mais peut mieux faire :

la hauteur du premier rectangle ? (1/5)²
moi je le trouve plutôt raplapla, pour un rectangle de hauteur (1/5)²

corrige et reviens me voir.

1/25

bravo

je te dis que (1/5)² n'est pas la bonne réponse, et tu me réponds 1/25, parce que évidemment, il y a une différence fondamentale entre (1/5)² et 1/25 ?

la hauteur du premier rectangle est 0, zéro, ZERO

il est aplati

le zéro te fait-il peur à ce point ?

je l'ai aime pas et je n'avais pas vu du coup le 2eme rectangle vaut (1/5)²  le 3 eme (2/5)²  le 4eme (3/5)²  et le 5eme (4/5)²

voilà

d'ailleurs, quand dans ta réponse erronée, tu donnais pour le cinquième rectangle la hauteur (5/5)² soit =1 (je te cite), tu aurais aussi pu remarquer que cela été faux.

Enfin, c'est quand même évident, sur le graphique, rassure-moi. Je ne suis pas le seul à le voir ?

tu as leur largeur, qui est la même pour tous : 1/5

tu as leurs hauteurs respectives.

Quelle est la surface de tous ces rectangles : la somme des surfaces de chacun.

Ca donne quoi ?

A toi.

l'aire d'un rectangle est longueur * largeur donc 1/5*0=0 pour le 1er rectangle
pour le 2eme revtangle c'est 1/5 * (1/5)²
pour le 3eme rectangle c'est 1/5 * (2/5)²
pour le 4eme rectangle c'est 1/5 * (3/5)²
pour le dernier rectangle c'est 1/5 * (4/5)²
apres on additionne chaque aire des rectangle et on obtient l'aire totale c'est sa????

c'est ça, avec un C cédille.

oui

et ça donne quoi ? (avec un C cédille)

tâche de factoriser de suite la largeur commune...

et compare avec s₅

sa nous donne 1/5((1/5)²+(2/5)²+(3/5)²+(4/5)²)

ce qui nous donne s5

maintenant je voudrait savoir comment on fait pour calculer l'aire au dessus de la parabole l'aire vert s'il vous plait

étonnant, n'est-ce pas ?
mais ces rectangles rouges ne couvrent pas toute la surface rose.



maintenant, on va faire la même chose, mais avec des rectangles qui dépassent la courbe, pour couvrir plus que la surface rose;



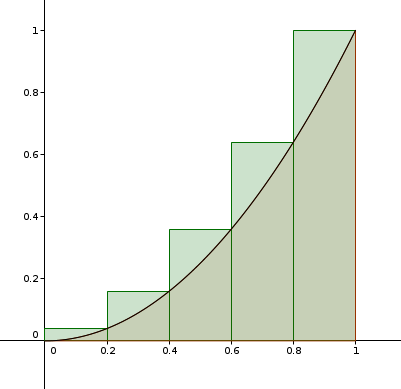
quelle sont leur largeur, leur hauteur, leur aire, la somme de leurs aires ?

pour le 5éme rectangle largeur 1/5 et hauteur 1
pour le 4eme rectangle largeur 1/5 et hauteur (4/5)²
pour le 3éme rectangle largeur 1/5 et hauteur (3/5)²
pour le 2eme rectangle largeur 1/5 et hauteur (2/5)²
pour le 1er rectangle largeur 1/5 et hauteur (1/5)²
ce qui nous donne 1/5*((1/5)²+(2/5)²+(3/5)²+(4/5)²+1)
C'EST SA

la question 1b je comprend pas ce qu'il faut faire:
L'unité d'aire étant celle du carré de côté 1, indiquez sur la figure l'aire associée à I(g5), celle associée à I(h5) puis celle associée ) la différence I(h5) - I(g5).
Ainsi "l'aire sous la parabole" P est encadrée par I(g5) et I(h5).

c'est ça, avec un C cédille

j'ai vu jusque sur mon écran ton visage s'illuminer.

ça fait plaisir.


question suivante ?

oui pour moi la question 1b est beaucoup trop vague qu'est ce qu'elle signifie au juste:
L'unité d'aire étant celle du carré de côté 1, indiquez sur la figure l'aire associée à I(g5), celle associée à I(h5) puis celle associée ) la différence I(h5) - I(g5).
Ainsi "l'aire sous la parabole" P est encadrée par I(g5) et I(h5).

oui, mes schémas te donnent la réponse.

la différence est la zone verte qui n'est pas recouverte par les rectangles rouges.

question suivante ?

ig5 est celleest celle en rose et ih5 est celle en vert
mais pour la difference ig5 - ih5 je dirai que c'est la parabole
et l'autre j'en est aucune idee

mais non,

la différence, c'est la différence

pourquoi chercher à compliquer ce qui est simple ?

ig5 c'est la surface des rectangles rouges
ih5 c'est la surface des rectangles verts
ih5 - ig5 c'est la différence des deux surfaces. c'est la partie des rectangles verts qui ne sont pas couverts par les rectangles rouges.

la surface rose, celle qu'on cherche, est supérieure à ig5 qui est la surface des rectangles rouges
et elle est inférieure à ih5 qui est la surface des rectangles verts.

Ainsi, on a un encadrement de la surface rose. tu sais ce que c'est, un encadrement en maths ?

je ne comprend pas du tout désolé
passons a la question suivantes:
On suppose n quelconque, n >(strictement) 2, et on pose sn = 1/n [f(0) + f(1/n) + ... + f(n-1 /n)].
Comme dans le cas n = 5, sn est la somme des aires des rectangles inférieurs, donc sn est l'intégrale d'une fonction en escalier définie par:

gn(x) = (k/n)² si x est dans l'intervalle ]k/n , k+1 /n[ avec 0 <(strictement) k <(strictement) n - 1.

De même, on pose Sn = 1/n [f(1/n) + f(2/n) + .... + f(n/n)]; Sn est la somme des aires des rectangles supérieurs, donc Sn est l'intégrale de la fonction en escalier hn définie par:

hn(x) = (k+1 / n)² si x est dans l'intervalle ]k/n , k+1 /n[ avec 0 <(strictement) k <(strictement) n - 1.

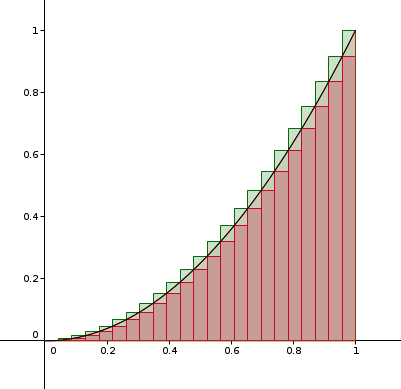
Prouver que sn = 1/n^3 [1² + 2² + .... (n-1)²] et Sn = 1/n^3 [1² + 2² + .... n²]

voilà

on fait la même chose, sauf que là, au lieu de découper la base en 5, on la découpe en 'n'.

donc le calcul fait intervenir 'n' là où tu trouvais des 5


il suffit d'écrire la somme



la somme va de 0 à 4, c'est à dire 5-1



on remplace les 5 par les 'n', avec des petits points pour dire qu'on ne peut pas écrire tous les termes, mais qu'ils sont là, dans les petits points.



et on factorise



d'où le résultat



ça, c'était , la somme des aires des 'n' rectangles rouges

tu fais la même chose avec , la somme des aires des 'n' rectangles verts.

et tu trouves

merci si bien de ton aide la 2 b est Exprimer sn et Sn en fonction de n. Démontrez que (sn) est une suite croissante et (Sn) une suite décroissante.

on fait comment si c'est par récurrence c'est meme pas la peine je m'entraine mais je ni arrive jamais

c'est bon je retrouve le meme resultat que toi maintenant passons a la question suivante qui est :

Exprimer sn et Sn en fonction de n. Démontrez que (sn) est une suite croissante et (Sn) une suite décroissante.

avec comme aide :

on rappelle que 1²+2²+...+k²= (k(k+1)(2k+1))/6

par récurrence ou par étude de la fonction réelle, mais les calculs sont longs et compliqués.

et il faut savoir que 1²+2²+..+n² = n(n+1)(2n+1)/6