Inscription / Connexion Nouveau Sujet
Allure d'une courbe paramétrée en un voisinage
Bonsoir
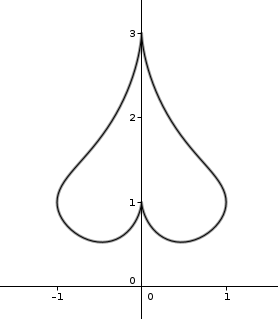
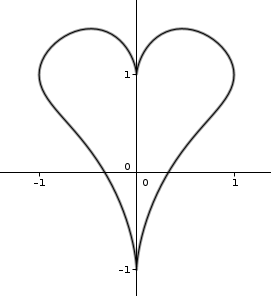
Donc voilà, j'ai x(t)=sin(t)^3 et y(t)=1+cos(t)-cos(t)^4
il faut étudier l'allure au voisinage de t=0
on me demande d'effectuer un DL3(0)de x et de y
x(t)=t^3+o(t^3)
y(t)=1+3/2t²+o(t^3)
au graphe de quelle fonction ressemble la courbe ?
j'hésite quant à comment obtenir la pente de la courbe...
je pensais faire (dy/dt)/(dx/dt) en utilisant les dl ( distance parcourue en ordonnée en un temps t divisé par la distance parcourue en abscisse en un même temps t... au voisinage de t=0)
(dy/dt)/(dx/dt)=(3x)/(3x²)=1/x donc la pente serait 1/x donc le graphe ressemblerait à ln
mais d'après une correction, la fonction devrait être 1+x^(2/3)
comment y parvient-on ? merci d'avance
Bonjour
"comment y parvient-on" : d'après tes dl, à peu de choses près, x, c'est t au cube, donc t, c'est x à la puissance 1/3, que tu reportes dans y.
mais j'ai comme l'impression qu'il y a une erreur de recopie soit dans ton énoncé soit dans ta correction ? le coeff 3/2 ne colle pas
le DL est exact
après on assimile la courbe à son DL et on dérive
dx/dt=3t²
dy/dt=3t
donc dy/dx=1/t et quand on tend vers une pente infinie, // axe des ordonnées
Ah en effet, la fonction devrait être 1+3/2x^(2/3)
merci je viens de comprendre
y=1+3/2t²=1+3/2(t^3)^(2/3)=1+3/2x^(2/3)
merci bcp !
pour la tangente et la position de la courbe par rapport à cette tangente, les dl suffisent :
x(t)=t^3+o(t^3)
y(t)=1+3/2t²+o(t^3)
si on appelle A le point de coordonnées (0;1), ça donne vecteur AM = 3t²/2 fois vecteur j + t^3 fois vecteur i + des pouièmes.
donc tangente dirigée par vecteur j (vers le haut), et si t négatif, on est un peu à gauche de cette tangente, si t positif un peu à droite.



 analyse en post-bac
analyse en post-bac