Inscription / Connexion Nouveau Sujet
Asymptote oblique
Bonjour
Soit la fonction
Comment peut on trouver l'équation de l'asymptote oblique a cette fonction ?
Merci
Skops

Bonjour Skops
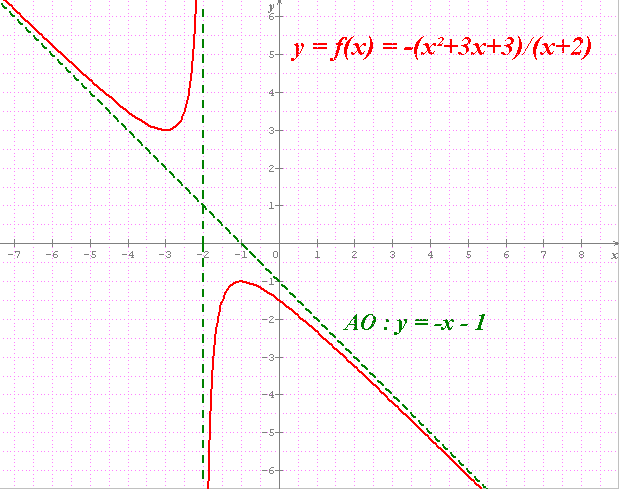
-x²-3x-3=-x(x+2)-x-3=-x(x+2)-(x+2)-5=(-x-1)(x+2)-5
f(x)=-x-1-5/(x+2) => f(x)->-x-1 qd x->oo
y=-x-1
AO
Philoux
Skops qui touche à tout les sujets 
Au fait j'ai acheté le bouquin que me proposait Nightmare, il a l'air complet, je vais avoir du boulot 
L'asymptote oblique j'ai pas vraiment pigé, rien que la définition ca me parait costaud...
La voila:
Si pour tout réel x appartenant à l'ensemble de définition de f, on a f(x)= ax + b + g(x) avec lim g(x) = 0 (en +oo ou -oo ) alors la droite d'équation y=ax+b est asymptote oblique à la courbe représentative de f en +oo ou -oo .
Bonne chance 

-x²-3x-3=-x(x+2)-x-3=-x(x+2)-(x+2)-5=(-x-1)(x+2)-1
f(x)=-x-1-1/(x+2) => f(x)->-x-1 qd x->oo
Ce qui ne change rien, même pas sur la position de la courbe / à son asymptote.
Philoux
Il faut rechercher y=ax+b tel que la différence
f(x)-(ax+b) tende vers 0 qd x->oo
Tu peux essayer ainsi aussi
Philoux
Salut Kevin
Merci pour l'explication 
Mais il faut y aller au feeling ou bien il y a des règles de calculs pour aboutir à ca ? 
PAr division polynomiale -x²-3x-3 / x+2, tu le trouves sans tatonner.
Par habitude, tu fais apparaitre, au numérateur le dénominateur, ce qui est (à mon avis) plus simple avec moins de risque d'erreur
Philoux
Autre chose importante et souvent demandé, c'est la position de la courbe par rapprt à son AO.
l'étude du signe de f(x)-(ax+b) te renseigne sur la position relative.
Philoux
Attention Skops
La différence f(x)-AO TEND VERS 0 pour |x|->oo
mais n'est pas =0.
AUtre chose :
Selon les courbes, il se peut que la courbe coupe son AO.
Une courbe peut couper son AO ailleurs qu'en oo !
Philoux
EN mettant (x+2) en facteur
Par ailleurs, comme dit un peu plus loin, remplaces le 5 par 1
Philoux
Ok merci philoux 
Je verrais ce chapitre ultérieurement, je termine les suites avant, faut pas que je brûle les étapes 
>>Skops
"Interro des lycées Maths 1ère S" , à la fnac 
Kevin

Après avoir mis (x+2) au num
j'ai récris la fraction en divisant par (x+2)
il reste alors :
f(x)= (-x-1) -1/(x+2)
où y = -x-1 est l'équ. de Asympt. Obl.
car f(x)->-x-1 qd |x|->oo
Ok ?
Philoux
Info> Il coute combien ?, oui en effet faut pas griller les étapes mais sa a ete une curiosité de savoir comment on faisait ca et puis aussi il n'ya avait plus personne a aider donc..., je crois que je vais faire les limites sans faire les asymptotes pour fini les suites et apres je me remmatrais au limites
Philoux > Heu pas ok
où y = -x-1 est l'équ. de Asympt. Obl.
car f(x)->-x-1 qd |x|->oo
Il est passé ou le -1 ?
>Skops
d'abord ce n'est pas -1
f(x) s'écrit sous la forme -x-1 -1/(x+2)
qd tu fais tendre |x| vers oo , -1/(x+2) td vers 0
=> la différence f(x)-(-x-1) tend vers 0+ ou 0-
ce qui défini l'AO
PLus clair ?
Philoux
>Sticky
Un plus simple ?
y=(x²+1)/x
Essaies, avec ce que tu sais, d'aller le plus loin possible dans l'étude de cette fonction
Df
parité
...
Ok?
Philoux
y=(x²+1)/x
Df=  -{0}
-{0}
Parité:
f(-x)= -(x²+1)/x = -f(x)
donc elle est impaire
ensuite limite?
x² tends vers +00, x+1 aussi
mais +00/+00 est une FI non? 
ca doit pas me servir
Son asymptote oblique passe par 0
J'avance 
Sticky

Dérivées:
(x²+1)'*1/x+-1/x²(x²+1)
= 2x*1/x+-1/x²(x²+1)
= 2- 1/x²(x²+1)
Meme si je vois pas trop si ca me sert
Sticky

Pour la limite en oo, Sticky, penses à écrire f(x) = (ax+b)+c/x
identifies a,b,et c (car ça fdoit être vrai pour tout x)
Sous cette forme, tu trouveras facilement la limite
Philoux
Le probléme Sticky , c'est que tu te bloques sur les formes indéterminés au lieu d'essayer de les contourner . Je te l'ai déja dit , une forme indéterminé n'indique pas forcément que la limite n'existe pas , au contraire

Jord
Ta dérivée est fausse Sticky
Pourquoi dis-tu que son AO passe par O ?
Le résultat est bon mais tu ne l'as pas justifié.
Philoux
Pour la limite en +00
f(x)=
donc
quand x tends vers +00 , 1/x tends vers 0
donc f(x) tends vers +00
sur -00
x tends vers -00, et 1/x, vers 0
donc f(x) tends vers -00
c'est ca?
Ou est l'erreur dans la dérivée?
Sticky

>Sticky
Pour trouver a,b et c, tu as deux méthodes :
soit tu "vois" que (x²+1)/x = x²/x +1/x = x + 1/x => a=1, b=0 et c=1
soit tu mets au même dén. : [(ax+b)x +c ]/x = (x²+1)/x
(ax²+bx+c)/x = (x²+1)/x si cela doit être vrai pour tout x alors les deux num. sont un même polynome :
ax²+bx+c=x²+1 =>
ax² identique à x² => a=1
bx identique à 0x => b=0
c identique à 1 => c=1
Philoux
Parfait pour la limite (post croisés)
pour la dérivé
as-tu vu (u/v)' ?
sinon dérives x+1/x c'est plus simple
Philoux
Bon alors je bugge enormement
je te le refais en latex et en détailler
Je ne vois pas comment utilise (u/v)'
en dérivant x+1/x
ca donne 1-1/x²?
bah attends, en devellopant l'autre on retrouve bien ca
oui je crois, donc c'est bon
merci
pour l'asymptote, il faut que le x "s'en aille" donc mon asymptote oblique est f(x)=x?
car
x-1/x² - x = -1/x² et -1/x² tends bien vers 0
Sticky

Oui Sticky
Tu vois que c'est plus simple (et moins risqué  ) de dériver x+1/x
) de dériver x+1/x
ta dérivée peut s'écrire (x²-1)/x²
tu dois pouvoir facilement avoir son signe en fonction de x
(Une question, j'ai un doute, ton profil dit 1° : tu es ou tu passes en 1° ?)
si c'est la deuxième réponse : bravo !
Philoux
Pourles dérivées, jai eu un bon prof (n'est ce pas ?  )
)
Ladérivée est toujours positive et donc, la fonctioon est toujours croissante.
Mais est ce que les dérivées m'aident pour les asymptotes?
Oui je passe en 1ere S  Merci
Merci 
(pourtant c'est marqué 2nd sur mon profil :s)
Sticky

behh.. si on cherche assez loin en effet on peut dire que les dérivées peuvent aider pour les asymptotes .
En effet , on peut obtenir l'asymptote d'une courbe (si elle existe) par un développement asymptotique , on peut arriver à ce développement avec la formule de Taylor-Young (si on a pas appris son tableau des développements limités usuels) , et cette formule utilise les dérivées (n-iéme) . Donc oui , ça peut aider  (bon on peut aussi utiliser mac laurin , n'est-ce pas Jérome ?
(bon on peut aussi utiliser mac laurin , n'est-ce pas Jérome ? 
 )
)

Jord
Oula, oui donc dans l'immédiat lol, ca ne sert pas 
Merci Nightmare 
et merci aussi à Philoux !!!
Sticky

Salut Sticky (20:06),
Pourles dérivées, jai eu un bon prof (n'est ce pas ? )
Ladérivée est toujours positive et donc, la fonctioon est toujours croissante
Pour la qualité du prof, je ne sais pas...
En revanche, ta conclusion sur le signe de la dérivée est fausse... 
revois mon post de 17:55
Si tu veux, on continue...
Cette fonction est riche et, même en pré-1°, bien encadré, tu peux aller loin...
Philoux
(x²-1)/x²
Oula, j'ai fait n'importe quoi 
Pour le prof, sisi, c'est sur ca par contre
alors
x² toujours positif, donc cela depend du signe de x²-1
donc
x²-1<0
(x+1)(x-1)<0
et pour l'autre
(x+1)(x-1)>0
Donc tableau de signe est donc
croissante sur ]-00;-1)U[1;+00[ et décroissante sur [-1;1]
Vouala
Pour ce qui est de continuer je suis d'accord:d
Sticky

Presque bon Sticky
La fonction n'est pas définie pour x=0 => décroissante par intervalles.
Un p'tit graphe en prime
Avec tout ce qu'on a dit (vu le titre du topic), vois-tu quoi faire pour déterminer l'AO ?
Philoux
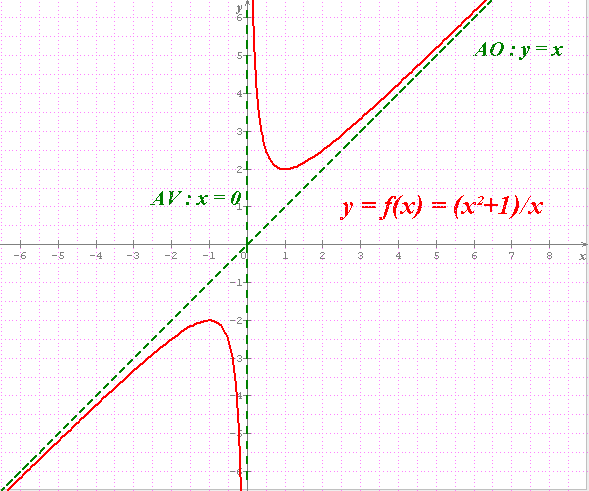
A mieux te relire, l'explication d'hier à 17:45 répondait à cette question.
J'ai oublié de te faire calculer les lim f(x) pour x->0- et 0+
Enfin quelle est la position de (C) par rapport à (AO) ?
Philoux
Ah ok donc décroissante sur [-1;0[ U ]0;1]
Bah deja, il fallait une fonction linéaire parce qu'elle passera par l'origine peut-etre parce qu'elle est impaire, je sais pas trop.
En utilisant f(x)=x+1/x, on regarde qu'elle fonction lineaire on peut soustraire pour que cela tende vers 0 donc x?
Sticky

Attention
Une AO ne passe pas OBLIGATOIREMENT par O(0,0) !
En revanche, l'imparité de f implique, en effet, celle de l'AO => AO passe par O(0,0)
Post croisés => lis 17:09
Philoux
Bon alors si j'ai encore un peu de memoire
lim f(x) pour x->0- et 0+
Limite de f(x) pour x qui tends vers 0 par des valeur négative, puis par des valeurs positive?
on va dire que oui
alors
j'ai f(x)=x+1/x
x tends vers 0- pour la premiere et donc 1/x tends vers 1/0- tends vers -00
dc le tout tends vers -00
Quand x tends vers 0+, 1/x tends vers 1/0+ dc +00
Donc le tout tends vers +00
Pour la position, je vois pas...
Sticky

Oui je sais que tout les AO ne passe pas par l'origine sinon, on dirait direct que f(x)-ax doit tendre vers 0 et pas ax+b
enfin je crois
Sticky

Penses à confirmer tes valeurs de limites par les sens de variations de f
Si tu avais trouvé limf=+oo qd x->0-, cela t'aurait "interpellé" avec le fait que f est décroissante sur -1,0[.
L'erreur peut être sur la limite ou le signe de f' => vérification des 2.
Quant à la position de (C) / (AO)
Pour un x donné, que représente f(x) - (x) ?
Philoux