Inscription / Connexion Nouveau Sujet
Barycentre : parallélisme et alignement
Bonsoir
Je demande un peu d'aide pour cet exercice:ABC est un triangle, G est le barycentre de (A, ),(B(
),(B( ),(C,
),(C, ),
), +
+ +
+
 0
0
 est la droite passant par A et parallèle à(BC). O désigne le milieu de [BC]
est la droite passant par A et parallèle à(BC). O désigne le milieu de [BC]
1 Démontrer l'affirmation suivante : "dire que G est un point de  ,équivaut à dire que
,équivaut à dire que  +
+ =0"
=0"
2 On suppose que  =2,
=2, =1,
=1, =-1
=-1
a) Justifier que (BG) coupe (AC) en un point J et que (CG) coupe (AB) en un point I.
b) Démontrer que les points O,I,J sont alignés
Pour 1 il faut montrer les 2 implications G 


 +
+ =0 si G
=0 si G 
 alors
alors  k tel que GA = k BC (en vecteur)En partant de la définition du barycentre et en remplaçant GA par k BC, peut-on arriver à le démontrer ?
k tel que GA = k BC (en vecteur)En partant de la définition du barycentre et en remplaçant GA par k BC, peut-on arriver à le démontrer ?
Pour 2)a peut-on passer par le trapèze GABC ?(diagonales et intersection des côtés non parallèles ?
Quant au b) je n'ai rien trouvé
merci
pour le 2 b) j'ai démontré que
G milieu de [BJ] et A milieu de [JC] du triangle BCJ puis comme
{[JO] était la 3ème médiane du triangle JBC donc passe par I.
C'est valable ?
Bonjour,
Pour la 1), tu peux regarder ici: ![]() Barycentre/centre d'inertie
Barycentre/centre d'inertie

2) On a
Supposons que
d' après 1), ce qui est manifestement faux.
donc et
sont sécantes en
Même raisonnement pour et
sécantes en

2)b) On peut démontrer que:
barycentre de
barycentre de
Considérons le barycentre de
Par associativité, on peut écrire:
barycentre de
Soit barycentre de
Donc , milieu de
, est en
et
sont alignés.

Merci beaucoup Cailloux de ton aide. Mais je ne comprends pas comment tu détermines K par bar de (I;2) (J,-1).
Re,
Evidemment, ça fait un peu parachuté (et pas doré) 
Par exemple, j' ai fait un petit dessin et j' ai conjecturé que
C' est à dire (ou
) barycentre de
Conjecture démontrée ensuite...
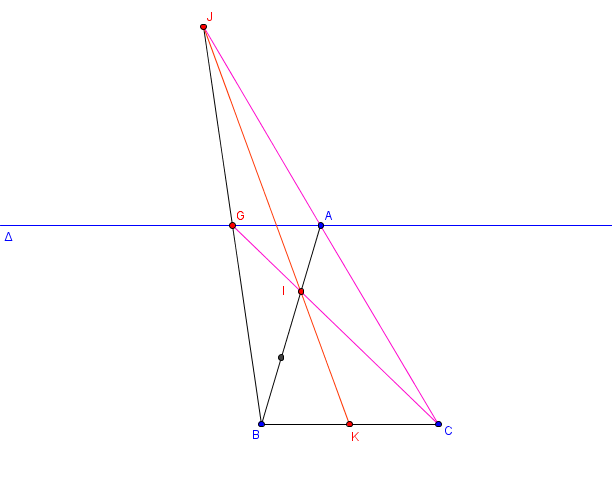

OK
En fait dans mon raisonnement je suis passée par les médianes
j'ai dit que G bar de A(2), B(1), C(-1) donc 2GA +GB-GC=0 (en vecteur)
J'introduis le point O :
2GA + GO +OB -GO-OC =0
soit 2GA +OB-OC =0
2GA +CB =0
GA = 1/2BC
Dans le triangle JBC ensuite j'applique Thalès JG/JB =JA/JC = GA/BC =1/2 Donc G milieu de JB, A mileu de JC donc [BA] et [GC] médiane du triangle BJC et se coupent en I, centre de gravité du triangle, donc [JO],troisième médiane passe par I
Je n'ai pas raisonné "barycentriquement parlant" et je voulais savoir si mon raisonnement était valable.
Merci encore
Ton raisonnement est parfaitement valable.
Au reste, ton exercice est axé sur les barycentres; je pense qu' il est préférable (mais pas indispensable) de démontrer l' alignement de 3 points en prouvant que l' un est barycentre des 2 autres.
Mais, je le répète, tu as tout juste! 


