Inscription / Connexion Nouveau Sujet
bonjour svp vous pouver maide c pour jeudi je comprend pas merci
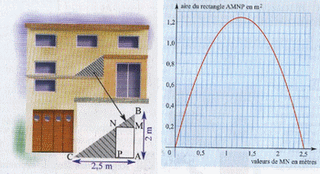
La figure ci-contre est une vue d'une maison de style moderne. Sur la partie hachurée, on veut placer une fenêtre représentée par le rectangle AMNP dans le triangle ABC.
Le but du problème est de déterminer les dimensions de la fenêtre ayant la plus grande aire possible.
ABC est un triangle rectangle en A tel que:
AB=2m et AC=2.5m.
N est sur [BC], M est sur[AB] et (MN) est parallèle à (AC).
On pose x=mn (distance exprimées en mètre.
première partie
1.En utilisant le théorème de Thalès, exprimer la distance BM en fonction de x.
En déduire que MA=2-o,8x
2.Calculer la hauteur MA de la fenêtre, puis son aire lorsque x=0.75
Même question pour x=1.
Pour quelle valeur de x la fenêtre est-elle carré?(Donner la valeur exacte, puis son arrondi au centimètre)
3.Pour des raisons d'esthétique, les dimensions de la fenêtre doivent respecter les condition suivantes:
.d'une part, la largeur MN doit être supérieure ou égale a 0.50m;
.d'autre part, la hauteur MA doit être supérieure ou égale à 0.60m.
Par le calcul, prouver que x doit alors vérifier:
0.50 ≤ x ≤ 1.75.
deuxième partie
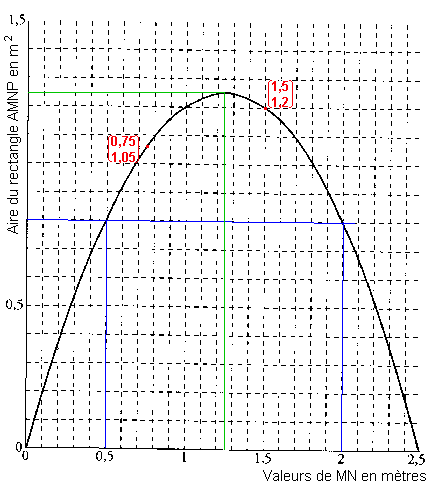
4.Sur le graphique ci-aprés, on a représenté l'aire du rectangle AMNP en fonction x.
Par simple lecture graphique:
a.Quelles sont les largeurs de la fenêtre correspondant à une aire de 0.80m²?, Pour ces largeurs, les conditions de la question 3 sont-elles vérifiées?
b.A quelle largeur correspond la fenêtre d'aire maximum? Pour cette largeur, comparer l'aire de la fenêtrte et l'aire du triangle ABC.
je vs remercie davance
waou tout ca ? c'est exactement que tu ne comprends pas ? tout ?
oué é sa c juste 1 exo jen né 2 de la mm longueur pour jeudi é je compren ri1 aider moi svp svp
1.En utilisant le théorème de Thalès,
BM/BA=NM/CA
BM=(BA*NM)/(CA)
BM=(2*x)/(2.5)
BM=2x/2.5=0.8m
J'en déduit que MA=2-0.8x
alors ?
2) l'aire d'un rectangle l*L
AM=2-0.8=1.8m
avec x=0.75
Aire=1.8*0.75=1.35m²
a toi de faire avec x=1
di moi si tu ne comprends pas
ciao et bonne rentreé
lol !
*=multiplier !
ok merci é eske ta compri le reste car moi je ne compren vrémen ri1 merci davance
mais tu as compris ce que je t'ai écrit ....
parce que pour le brevet y'aura que des trucs comme ca ... lol
c'est pas pour te casser le moral ...
2)avec x=1
Aire=1.8*1=1.8m
pour x=1 la fenetre est carré
bon courage pour le reste ....
AHHHH mince !!!! je suis désolé je me suis gouré mais suffit juste que tu change les chiffres sinan les calcules sont bon 
dis moi si c'est pas bon ...
je pe pa tu dire si c juste ou pa kar g ri1 compri lol é eske tu arive le reste ?
2) l'aire d'un rectangle l*L
AM=2-0.8=1.2m
avec x=0.75
Aire=1.2*0.75=1.35m²
avec x=1
Aire=1.2*1=1.2m
pour x=1 la fenetre est carré car la longueur et la largeur est de 1.2m
voilà g corrigé
pour le reste je ne peux pas t'aider je dois y aller
demande à quelqu'un
mé 1.2*0.75=0.9 non?
La figure ci-contre est une vue d'une maison de style moderne. Sur la partie hachurée, on veut placer une fenêtre représentée par le rectangle AMNP dans le triangle ABC.
Le but du problème est de déterminer les dimensions de la fenêtre ayant la plus grande aire possible.
ABC est un triangle rectangle en A tel que:
AB=2m et AC=2.5m.
N est sur [BC], M est sur[AB] et (MN) est parallèle à (AC).
On pose x=mn (distance exprimées en mètre.
première partie
1.En utilisant le théorème de Thalès, exprimer la distance BM en fonction de x.
En déduire que MA=2-o,8x
2.Calculer la hauteur MA de la fenêtre, puis son aire lorsque x=0.75
Même question pour x=1.
Pour quelle valeur de x la fenêtre est-elle carré?(Donner la valeur exacte, puis son arrondi au centimètre)
3.Pour des raisons d'esthétique, les dimensions de la fenêtre doivent respecter les condition suivantes:
.d'une part, la largeur MN doit être supérieure ou égale a 0.50m;
.d'autre part, la hauteur MA doit être supérieure ou égale à 0.60m.
Par le calcul, prouver que x doit alors vérifier:
0.50 ≤ x ≤ 1.75.
deuxième partie
4.Sur le graphique ci-aprés, on a représenté l'aire du rectangle AMNP en fonction x.
Par simple lecture graphique:
a.Quelles sont les largeurs de la fenêtre correspondant à une aire de 0.80m²?, Pour ces largeurs, les conditions de la question 3 sont-elles vérifiées?
b.A quelle largeur correspond la fenêtre d'aire maximum? Pour cette largeur, comparer l'aire de la fenêtrte et l'aire du triangle ABC.
je vs remercie davance
** image supprimée **
*** message déplacé ***
bonjour,
pas de multipost. Merci ![]() bonjour svp vous pouver maide c pour jeudi je comprend pas merci
bonjour svp vous pouver maide c pour jeudi je comprend pas merci
Pookette 
*** message déplacé ***
Je ne vérouille pas mais premier et dernier avertissement...

La figure ci-contre est une vue d'une maison de style moderne. Sur la partie hachurée, on veut placer une fenêtre représentée par le rectangle AMNP dans le triangle ABC.
Le but du problème est de déterminer les dimensions de la fenêtre ayant la plus grande aire possible.
ABC est un triangle rectangle en A tel que:
AB=2m et AC=2.5m.
N est sur [BC], M est sur[AB] et (MN) est parallèle à (AC).
On pose x=mn (distance exprimées en mètre.
première partie
1.En utilisant le théorème de Thalès, exprimer la distance BM en fonction de x.
En déduire que MA=2-o,8x
2.Calculer la hauteur MA de la fenêtre, puis son aire lorsque x=0.75
Même question pour x=1.
Pour quelle valeur de x la fenêtre est-elle carré?(Donner la valeur exacte, puis son arrondi au centimètre)
3.Pour des raisons d'esthétique, les dimensions de la fenêtre doivent respecter les condition suivantes:
.d'une part, la largeur MN doit être supérieure ou égale a 0.50m;
.d'autre part, la hauteur MA doit être supérieure ou égale à 0.60m.
Par le calcul, prouver que x doit alors vérifier:
0.50 ≤ x ≤ 1.75.
deuxième partie
4.Sur le graphique ci-aprés, on a représenté l'aire du rectangle AMNP en fonction x.
Par simple lecture graphique:
a.Quelles sont les largeurs de la fenêtre correspondant à une aire de 0.80m²?, Pour ces largeurs, les conditions de la question 3 sont-elles vérifiées?
b.A quelle largeur correspond la fenêtre d'aire maximum? Pour cette largeur, comparer l'aire de la fenêtrte et l'aire du triangle ABC.
je vs remercie davance
** image supprimée **
*** message déplacé ***
La figure ci-contre est une vue d'une maison de style moderne. Sur la partie hachurée, on veut placer une fenêtre représentée par le rectangle AMNP dans le triangle ABC.
Le but du problème est de déterminer les dimensions de la fenêtre ayant la plus grande aire possible.
ABC est un triangle rectangle en A tel que:
AB=2m et AC=2.5m.
N est sur [BC], M est sur[AB] et (MN) est parallèle à (AC).
On pose x=mn (distance exprimées en mètre.
première partie
1.En utilisant le théorème de Thalès, exprimer la distance BM en fonction de x.
En déduire que MA=2-o,8x
2.Calculer la hauteur MA de la fenêtre, puis son aire lorsque x=0.75
Même question pour x=1.
Pour quelle valeur de x la fenêtre est-elle carré?(Donner la valeur exacte, puis son arrondi au centimètre)
3.Pour des raisons d'esthétique, les dimensions de la fenêtre doivent respecter les condition suivantes:
.d'une part, la largeur MN doit être supérieure ou égale a 0.50m;
.d'autre part, la hauteur MA doit être supérieure ou égale à 0.60m.
Par le calcul, prouver que x doit alors vérifier:
0.50 ≤ x ≤ 1.75.
deuxième partie
4.Sur le graphique ci-aprés, on a représenté l'aire du rectangle AMNP en fonction x.
Par simple lecture graphique:
a.Quelles sont les largeurs de la fenêtre correspondant à une aire de 0.80m²?, Pour ces largeurs, les conditions de la question 3 sont-elles vérifiées?
b.A quelle largeur correspond la fenêtre d'aire maximum? Pour cette largeur, comparer l'aire de la fenêtrte et l'aire du triangle ABC.
merci davance
** image supprimée **
*** message déplacé ***
3ème multipost ![]() bonjour svp vous pouver maide c pour jeudi je comprend pas merci + multi comptes !!
bonjour svp vous pouver maide c pour jeudi je comprend pas merci + multi comptes !!
merci aux modérateurs de verrouiller ce topic
Pookette 
*** message déplacé ***
J'ai vu ya 2-3 truc faux donc voici les réponses (100% juste)
1) En utilisant le théorème de Thalès, exprimer la distance BM en fonction de x. En déduire que MA = 2 - 0,8x
Dans le triangle ABC, (MN) est parallèle à (AC).
En utilisant l'application du théorème de Thalès au triangle, nous avons les égalités suivantes :
Remplaçons MN par x et les données connues par leurs valeurs :
Nous en déduisons que et que MA = AB - BM = 2 - 0,8 x.
2) Calculer la hauteur MA de la fenêtre puis son aire lorsque x= 0,75. Même question pour x = 1,5. Pour quelle valeur de x la fenêtre est-elle carrée ?
Lorsque x = 0,75, MA = 2 - 0,8 x 0,75 = 2 - 0,6 = 1,4 ; l'aire de la fenêtre est 1,4 x = 1,4 x 0,75 = 1,05 m2.
Lorsque x = 1,5, MA = 2 - 0,8 x 1,5 = 2 - 1,2 = 0,8 ; l'aire de la fenêtre est 0,8 x = 0,8 x 1,5 = 1,2 m2.
La fenêtre est carrée lorsque 2 - 0,8 x = x soit x + 0,8 x = 2 ; 1,8 x = 2 donc
3) Placer sur la courbe les points correspondant aux calculs de la deuxième question.
( voir attachement)
4) Par le calcul, prouver que x doit alors vérifier : 0,50 x 1,75.
Si MN 0,50 m, nous avons x 0,50.
Si MA 0,60, nous avons 2 - 0,8 x 0,60 ou 0,8 x 2 - 0,60 donc .
La combinaison de ces deux conditions donne l'encadrement 0,50 x 1,75
5) a) Quelles sont les largeurs de fenêtre correspondant à une aire de 0,80 m2 ? Pour ces largeurs, les conditions de la question 4) sont-elles vérifiées?
Sur le graphique, on voit qu'une aire de 0,8 m2 peut être obtenue par une valeur de x proche de 0,5 mètre une valeur proche de 2 mètres. Ces valeurs ne sont pas dans la fourchette voulue pour la valeur de x.
b) A quelle largeur correspond la fenêtre d'aire maximum ? Pour cette largeur, comparer l'aire de la fenêtre et l'aire du triangle ABC.
Sur le graphique, on voit que l'aire maximale est d'environ 1,25 m2 et est obtenue pour une valeur de x d'environ 1,25 m.
L'aire du triangle ABC est , elle est le double de celle trouvée pour la fenêtre.
Source : http://www.crdp.ac-grenoble.fr/imel/brevet/brevet97/rennes/solpb.htm
c'es le corriger du Brevet des collèges de 1997