Inscription / Connexion Nouveau Sujet
Courbe de Bézier
Bonjour excusez moi de vous déranger mais j' ai un DM pour les vacances et je ne comprend absolument rien ! Avant de poster un nouveau topic, j' ai cherché si il n' existait pas, il y en a des similaires mais impossible à comprendre.
Mon DM portait sur une construction géogebra :
1) CONSTRUCTION
Dans l' ordre j' ai fait cela :
- construit 3 points A B et c
- créée une variable t dans l' intervalle [0,1]
- créée les barycentres
G=bar((A,1-t),(B,t)) ,
H=bar((B,1-t),(C,t))
et M=bar((G,1-t),(H,t))
- créée les segment [AB], [BC] et [GH]
- puis j' ai fait varier t dans l' intervalle [0,1]
Ensuite, on me demande une conjecture. En classe, nous avons donné cette conjecture :
Il semble que ce soit un bout de parabole
2) DÉMONSTRATION DANS UN CAS PARTICULIER
a ) déplacer les 3 points de départs tel que A(-3/2,0) , B(-1/2,16) et C(1/2,0)
b) conjecturer une équation de la courbe obtenue
c) déterminer les coordonnées de M en fonction de t puis vérifier la conjecture
d) déterminer le rôle des droites (AB) et (BC)
Je vais essayer de joindre quelque étape de ma construction
Je suis désolé de balancer ca comme cela mais vraiment je suis perdu je comprend pas du tout.
Je vous remercie vraiment beaucoup si vous pouvez m' accorder un peu de votre temps pour m' aider si ca dérange personne.
Bonsoir,
Il faut commencer par écrire les coordonnées de G et H.
xG=-(3/2)(1-t)-t/2
yG=16t
xH=-(1/2)(1-t)+t/2
yH=16(1-t)
Une fois ces expressions simplifiées, on écrit les coordonnées de M
xM=(1-t)xG+txH
yM=(1-t)yG+tyxH
En développant, on trouve l'équation d'une parabole.
Vraiment désolé j' avais pas vu que quelqu' un m' avais répondu je suis nouvelle j' ai encore du mal. Merci de m' avoir répondu, je vais étudier ce que vous m' avez envoyé et je vous redit si je trouve la solution. Merci beaucoup en tout cas
Bonjour . Je suis débordé de devoirs je viens de faire ce que vous m' avez indiquer , j' ai simplifié les coordonnées de G et H, mais je sais pas si j' ai bon, car lorsque, par exemple il y avait 16 en facteur, j' ai développé .. au final j' ai :
xG=-3/2 + t
yG= 16t
xH=t/2
yH=16 - t
donc les coordonnées de M donne :
x M = (1-t)(-3/2+t) + t(t/2)
= -3/2 + t + 3t/2 -t² + t²/2
= -3/2 + 2t/2 + 3t/2 - 2t²/2 + t²/2
=-3/2 +5t/2 - t²/2
y M = (1-t)16t + t(16-t)
= 16t - 16t² + 16 - t²
= 16t - 17t² + 16
Voilà ! J' ai bon déjà ?
Ensuite pour trouver l' equation il faut que je résolve ( je ne sais pas si ca ce dit ainsi .. ) une equation a 2 inconnues..
y=ax+b
16t-17t²+16 = a( -3/2 + 5t / 2 - t² / 2 ) + b
Hmm .. je bloque
Oui en effet je trouve -1/2 + t donc c 'est bon. Je refais les calculs.
Mais en faite, comment avec les coordonnées ont peut trouver l' equation ?
J'ai trouvé la même chose 
Il reste à écrire t=(xM+3/2)/2 et à le remplacer dans l'expression de yM
Ensuite, il faut transformer l'équation pour faire apparaitre l'équation d'une parabole sous la forme y=ax²+b
Voilà, alors je trouve t = (2xM + 3 ) / 4
et donc yM = 32((2xM + 3) / 4 ) - 32 ((2xM + 3) / 4)²
Je suis ennuyeuse mais je n' arrive pas à developper pour yM
Bonjour,
Tu ne m'ennuies pas, rassure-toi 
J'ai dû m'absenter hier soir.
Voici ce que j'ai trouvé
Finalement, on obtient
Il s'agit bien d'une parabole de sommet (-1/2;8) et tournée vers le bas.
Pour t, je trouve pareil sauf que ensuite j' ai multiplié par l' inverse, mais bon ce n' etait pas necessaire.
Pourquoi 32t(1-t) on ne le developpe pas en 32t-32t²? ce n' est pas plus simple ?
je ne comprend pas cette partie la : (1/4 - xM/2 ) ? ni la suite d' ailleurs . Je vais essayer de comprendre
Je n'ai pas développé 32t(1-t) parce que les calculs sont plus compliqués que si on remplace directement t et 1-t par leurs expressions en fonction de xM
donc
Ahh d' accord !! Je comprenais pas ! Merci beaucoup. Donc la on a prouver la question 3 ? Je vais essayer de tout refaire toute seule sans regarder le forum !
Merci énormement énormement !
Ensuite il faut prouver que (AB) et (BC) sont des tangentes. Je vais essayer, il faut utiliser les dérivés je pense. Je vais essayer toute seule je vous dis si je n' y arrive pas , enfin si cela ne vous dérange psa ?
En développant l' equation, je suis arrivée à une equation du seconde degré : -8x²-8x + 6
Je vais déterminer sa dérivée
Je pense que vous vous êtes trompé... la parabole est tournée vers le haut plutôt non ? Et comment savez vous que le sommet est au point (-1/2;8) ?
Bonjour xAmel,
Non, il n'y a pas d'erreur (voir la courbe ci-dessous).
A partir de f'(x), on peut écrire les équations des tangentes aux points A et C grâce à la formule (à connaitre par coeur) y=f'(a)(x-a)+f(a) où a représente l'abscisse du point où s'applique la tangente.
Une fois que tu auras déterminé les équations des tangentes en A et en C, il faut montrer que B appartient à ces deux droites.
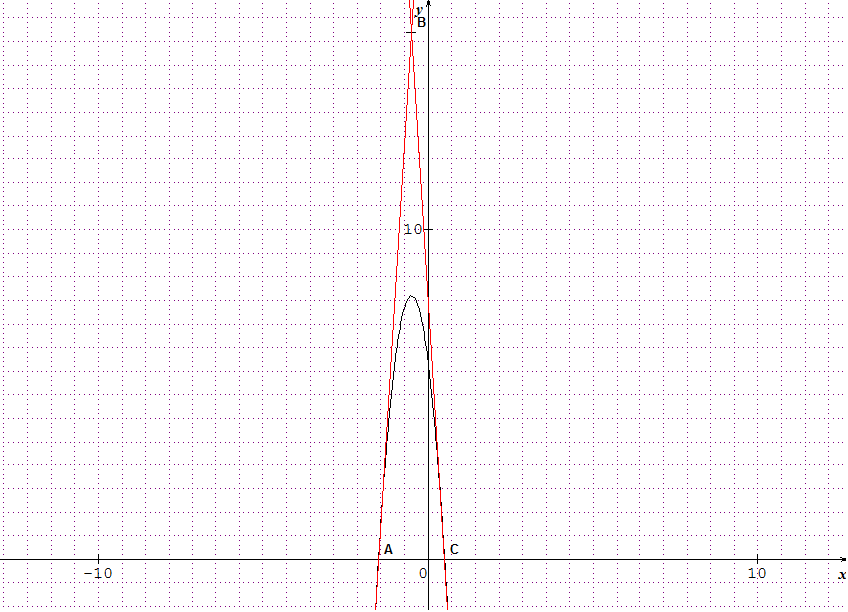
ah oui en effet j' avais celle ci je pensais que tournée vers le bas voulais dire l' inverse ! Merci !
Je vais étudier ce que vous m' avez dit !
1000 mercis !!
Juste une simple question, a c' est - 3/2 et 1/2 ? on a pas besoin de le démontrer ?
et pourriez vous me dire comment avez vous détemriner le point du sommet de la parabole ? Juste pour moi, pour que je le sache pour une prochaine fois ?
Voilà, l' equation de la tangente en A est : y = 16x + 24
" " " en B est : y = -16x + 8
Ensuite je dois faire : 16 = 16 * -1/2 + 24
16 = -16 * -1/2 + 8 ?
Plutôt que d'arriver à 0=0, il vaut mieux remplacer x par -1/2 dans chaque équation et trouver que y=16, ce qui permet de dire que le point B(-1/2;16) appartient à chacune des 2 droites.
Puisque A appartient déjà à la tangente en A (par définition), le fait de montrer que B appartient aussi à cette tangente montre que la droite (AB) est la tangente (puisqu'une droite est définie par 2 points).
Pareil pour (BC)
Oui, c'est fini. Tu peux aller profiter du beau temps (j'espère qu'il y en a chez toi).
Moi, c'est ce que je vais faire.
Bon dimanche !



