Inscription / Connexion Nouveau Sujet
DEFI 7 : Le mathilien fou.


Bonjour à tous, nouveau défi, géométrique cette fois.
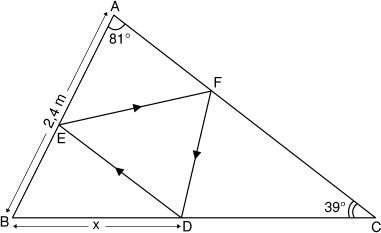
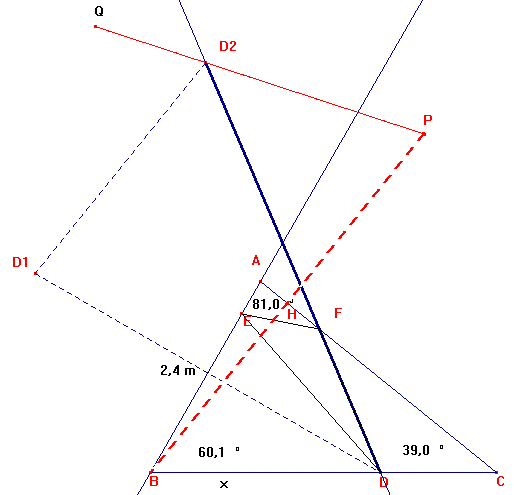
A force de passer trop de temps sur l'île, un ancien mathilien est devenu fou. Il s'est donc retrouvé enfermé dans une cellule capitonnée triangulaire. (Figure jointe.)
Comme tout bon aliéné, il se cogne la tête contre les murs de sa cellule mais étant donné qu'il est légèrement obsessionnel, il souhaite optimiser son parcours en empruntant toujours le même circuit. Il part du point D sur le mur [BC] puis va se cogner en E sur le mur [BA], en F sur le mur [AC] et revient en D pour un deuxième tour et ainsi de suite...
De plus, il choisit le circuit qui lui permettra de se cogner le plus de fois possible, autrement dit le circuit le plus court.
A quelle distance x du point B doit-il alors choisir son point de départ ?
(On donnera la valeur en centimètres, éventuellement arrondie au millimètre.)
Bonne réflexion.
minkus
 Bonjour,
Bonjour,
il me semble qu'il s'agit là d'un problème classique : minimiser le périmètre d'un triangle inscrit dans un triangle donné.
Sauf que la première question qui m'est venue à l'esprit était de savoir si, après s'être cogné, le fou errant "rebondit", comme dans le cas d'une réflexion, avec un angle d'incidence égal à celui d'entrée... ce qui pourrait donner deux versions de réponses possibles !
(à moins que la précision toujours le même circuit soit sensée induire la réfléxion usuelle ?)
Mais en réalité, il n'en n'est rien car les deux cas coïncident: Sans utiliser de condition angulaire, le triangle de périmètre minimal vérifie automatiquement les conditions de la réflexion usuelle. C'est bien un fou de l' !
! 
Enfin, la résolution:
Pour commencer je considère (encore une méthode classique dans les problèmes de plus court chemin), les symétriques D' et D" de D par rapport aux côtés [AB] et [AC]. Le périmètre du triangle sera alors minimal si et seulement si les points D',E,F et D" sont alignés, ce qui peut s'écrire (d'après l'inégalité triangulaire) D'D"=D'E+EF+FD" ou encore D'D"=DE+EF+FD=p le périmètre du triangle DEF.
Les calculs (un peu longs) conduisent, en particulier à l'aide de la formule des sinus,
à une longueur x égale à cm (valeur exacte) pour un périmètre p=
.
Merci pour l'énigme.
NB: Autre méthode ? Le point D est le pied de la hauteur issue de A, x=2,4cos 60°!
 Ce problème revient à celui de la construction du triangle de périmètre minimal dont les sommets appartiennent aux côtés d'un triangle initial ABC, dont les angles sont aigus.
Ce problème revient à celui de la construction du triangle de périmètre minimal dont les sommets appartiennent aux côtés d'un triangle initial ABC, dont les angles sont aigus.
C'est le triangle "orthique" de ABC.
C'est le triangle qui joint les pieds des hauteurs du triangle ABC.
On a donc x=2,4*cos(ABC)
L'angle (ABC) est égal à 180°-(81°+39))= 60°
x= 2,4*0,5 =1,2m = 120cm
 re,
re,
Désolé pour cette réponse complètement idiote!
Beaucoup trop de précipitation!
Je posterai plus tard une réponse plus sensée.



Salut, voici ma réponse: x = 60 cm.
le triange DEF de périmètre minimum inscrit dans le triangle ABC est le triangle orthique, c'est-à-dire de sommets les pieds des hauteurs, donc D est le pied de la hauteur issue de A. D'où BD = AB cos 60° = AB/2 = 1,2 m = 60 cm.
 la distance x du point B est de 120 cm.
la distance x du point B est de 120 cm.
Il devra ensuite se diriger vers AB sous un angle de 81° par rapport à BC, puis aller vers AC sous un angle de 39° par rapport à AB.
 Pour optimiser son parcours, le mathilien fou doit se cogner la tête au niveau des hauteurs du triangle.
Pour optimiser son parcours, le mathilien fou doit se cogner la tête au niveau des hauteurs du triangle.
L'angle ABC vaut 60° donc x = 2,4 m / 2 = 1,2 m.
x = 120,0 cm
 Bonjour
Bonjour
Expérimentalement j'ai trouvé que D devait être le pied de la hauteur issue de A avec E = F = A et BD = x = 240.cos(60°) = 120 cm (la démonstration viendra sans doute plus tard ) donc je dirais
A+



 Pour parcourrir le chemin le plus court possible, il me semble qu'il doit se cogner aux points de contacts entre le cercle inscrit et les côtés du triangle.
Pour parcourrir le chemin le plus court possible, il me semble qu'il doit se cogner aux points de contacts entre le cercle inscrit et les côtés du triangle.
Pour trouver la longueur BD, j'utilise donc le triangle de Gergonne quui me donne :
BD=(AB+BC-AC)/2
et je trouve BD=143,2cm (en arrondissant au millimètre supérieur)
Sur ce défi, je ne suis pas très sûre de ma réponse alors j'attends le verdict...
 Bonjour,
Bonjour,
Le mathilien fou doit choisir son point de départ à une distance du point B.
Il devra décrire ensuite un circuit correspondant au triangle orthique DEF du triangle ABC formant la cellule capitonnée.
Pour info, le circuit fait environ 410,6 cm (arrondi au mm  )
)
Merci Minkus pour ce défi très instructif.
A+, KiKo21.



 Bonsoir !
Bonsoir !
Aussi fou soit-il, notre ancien mathimilien aura vite calculé qu'il doit commencer son trajet à une distance du point B. (Distance donnée en cm comme le demande l'énoncé et il n'est pas nécessaire d'arrondir : c'est une valeur exacte.)
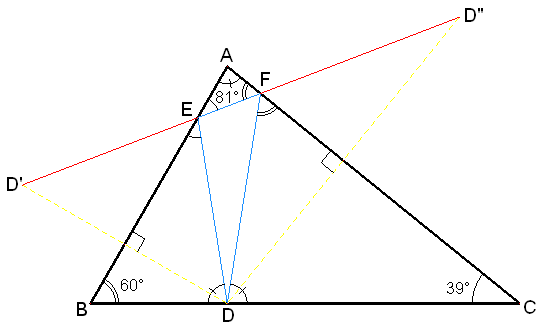
Si on lui pose la question, notre mathimilien répondra qu'il ne se cogne pas aux murs : il les traverse ! (Il faudrait être fou pour se cogner la tête aux murs !) A chaque fois qu'il traverse un mur, il se retrouve dans une nouvelle cellule, identique à la sienne mais symétrique par rapport au plan du mur traversé !! Et bien sûr pour optimiser son parcours, il avance toujours en ligne droite.
Traduction : sur le schéma joint, on a représenté le triangle de la cellule et son symétrique par rapport au côté [AB] puis le symétrique du symétrique par rapport au côté image [A'C']. Un parcours fermé D->E->F->D a pour image le parcours (de même longueur) D->E->F'->D'', où D'' est l'image de D par les deux symétries. Pour D fixé, D'' l'est également, et le plus court chemin entre les deux est bien entendu la ligne droite. E et F' doivent être sur le segment [DD''] ce qui nous permet d'identifier un chemin fermé optimal pour D fixé. Reste à placer D pour réduire au maximum la longueur DD''...
Poursuite de l'interrogatoire : notre mathimilien non seulement persiste à affirmer qu'il traverse les murs tout droit, mais il prétend de surcroît avoir "optimisé" son parcours ! L'explication est pour le moins farfelue et témoigne de son degré de folie : il dit se placer au pied de la hauteur du sommet qu'il nomme "A" de sa cellule, dos au mur, puis se tourner de 9° vers la gauche et filer tout droit ! Il parle à toute vitesse : "C'est le trajet minimum ! Toutes les deux cellules, j'effectue une rotation de 162 degrés ! 180° = 162° + 9° + 9° ! En me plaçant au pied de la hauteur, je minimise mon parcours ! En suivant un angle de 9°, je me retrouve à mon point de départ après avoir traversé trois cellules et marché 4.10m !"
Traduction : La composée de deux symétries est une rotation. Le triangle AB''C' est l'image du triangle ABC par rotation de centre A et d'angle 2*81 = 162° (dans le sens indirect). En particulier le trajet D vers D'' suit la base d'un triangle isocèle de sommet A, d'angles 9° et 162° au sommet. La distance de D vers D'' est donc directement proportionnelle à la longueur AD. Minimiser DD'' revient à minimiser AD c'est à dire à choisir D le pied de la hauteur de sommet A du triangle ABC. Comme l'angle au sommet B vaut 60°, il faut choisir AD = x = 1/2 * 2.4m = 1.2m. On peut calculer la longueur du trajet optimal : DD'' = 2 * cos(9°) * sin(60°) * 2.4m ~ 4.106m.
Merci pour cette énigme qui a été l'occasion d'exploiter les ressources de Geogebra ! (Formidable outil d'aide à la résolution !  )
)
 Si j'ai bien compris l'énoncé, il faut trouver le triangle DEF de périmètre minimal.
Si j'ai bien compris l'énoncé, il faut trouver le triangle DEF de périmètre minimal.
Sauf erreur il s'agit du triangle dont les sommets sont les pieds des hauteurs du triangle ABC.
Comme angle(ABC)=60° alors je trouve



 Bonjour,
Bonjour,
Je me suis rendu compte après avoir posté que j'ai introduit un nouveau vocable dans l'île : mathimilien ! 
Erreur involontaire qui je l'espère ne me vaudra pas un poisson ! 
 Bonjour et merci pour cette énigme
Bonjour et merci pour cette énigme
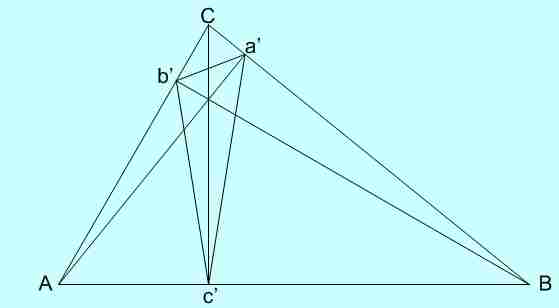
Je pense que le triangle le plus petit (du point de vue périmètre) est celui formé par les points a', b' et c' issus des 3 hauteurs. (voir schéma)
Ainsi, ma réponse est X = 120 cm
Maintenant, ça me parait assez simple pour une 3 étoile et j'ai peur de passer à coté.
Mais vu que la course au titre est cuite pour moi ce mois-ci, je tente.
A bientôt!
Pour info, je trouve un périmètre de 410.5744 cm
 31.9 cm
31.9 cm
Pour trouver ce résultat, j'ai utilisé un principe assez connu, celui du cheval qui a soif et qui doit aller dans une ville.
Vous ne connaissez pas?
Soit D une droite représentant une rivière et C un point du plan représentant un cheval, V un point du plan du même côté de la rivière que C représentant la ville.
Le cheval a soif et doit aller à la ville. Il veut donc faire un tour à la rivière avant d'aller à la ville.
Il va évidemment se déplacer de telle manière à minimiser son trajet. Où va t-il donc boire sur la rivière?
Version mathématique: Comment trouver le point X de D minimisant la distance CX+XV ?
A la fin de la résolution (par symétrie, c'est assez joli), on s'aperçoit que le cheval a, vu de dessus, "rebondi" sur la rivière, les angles d'arrivée et de départ sont égaux. En fait, c'est une condition nécessaire de minimisation de trajet.
Dans cette énigme, il suffit donc de trouver un triangle inscrit dans le gros triangle de telle sorte que à chaque sommet du nouveau triangle, les angles de part et d'autre soient égaux.
Je laisse l'explications des détails aux autres... cf démo de borneo plus haut



 Bonjour.
Bonjour.
Je trouve x = 2.4(sin81/sin39-sin60cotan39+cos81cos39)/(1+cos60cos81cos39)
soit x = 140.6 cm
A+
 Bonjour à tous,
Bonjour à tous,
Notons d'abord que l'angle B mesure 180° - 81° - 39° = 60°.
Le point D se trouve à 240 cm x cos 60° = 240 cm x 0,5 = 120 cm du point B.
Le point D est le pied de la perpendiculaire abaissée du sommet A sur le côté (BC), et l'un des 3 sommets du triangle orthique ( triangle pédal de périmètre minimal).
atomium.
 Le triangle DEF est le triangle orthique du triangle ABC.
Le triangle DEF est le triangle orthique du triangle ABC.
Les points D, E et F sont les hauteurs du triangle ABC issues respectivement de A, C et B.
La distance recherchée vaut 240 * sin(180°-81°-39°) = 240 * sin(60°) soit 120 cm.
A+,
gloubi
 re-Bonjour,
re-Bonjour,
Un doute affreux m'envahi... J'ai posté sinus ou cosinus? C'est cosinus, évidemment, pour que le résultat soit 120 cm!
Pourtant je m'étais relu. comme quoi...
A+,
gloubi



 Bonjour,
Bonjour,
Les énigmes de géométrie… là je coince vraiment. En général elles sont souvent notées de 3 ou 4 étoiles, alors pour rester dans la course au titre (…que NF2 gagnera certainement encore cette fois), j'ose une réponse.
Voilà ma proposition (dont je ne suis absolument pas sûr) : je suppose (sans confirmation mathématique, mais cela ne me paraît pas si mal comme approche) que pour trouver le chemin le plus court, les trois triangles AEF, BDE et FDC sont isocèles, leurs côtés égaux étant les segments du triangle ABC.
A partir de là, je retrouve tous les angles de la figure proposée par Minkus. Puis à l'aide de la formule :
a / sin A = b / sin B = c / sin C (formule que j'ai trouvée sur Internet), on arrive à déduire la valeur de X.
Je propose ainsi : X = 143.2 cm.
Merci pour cette énigme, qui sent fortement le poisson…
 Bonjour
Bonjour
N'étant pas (encore !) parvenu à trouver une solution géométrique ou analytique valable , je me suis tourné vers une méthode graphique à l'aide de Cabri pour trouver comme dans mon post précédent mais cette fois E est tel que AE
 424cm et F est tel que AF=
424cm et F est tel que AF= 320cm
320cm
En fait tout bêtement j'ai fait voyager D, E et F sur leur côté respectif en regardant la longueur du périmètre de triangle DEF et je me suis arrèté au minimum.
Ca sent le 
Mais on verra
A+
 Rebonjour
Rebonjour
Correction de mon post du 17/05/ de 10h01 ; c'est AE = 4,24 cm et AF = 3,20 cm
les virgules s'étaient envolées.
A+
 Rerebonjour
Rerebonjour
Décidément c'est pas mon jour : trop précipité
en définitive AE = 42,4 cm et AF = 32 cm (ce n'est qu'une question de virgule)
Encore sorry.
A+
 Salam,
Salam,
A en croire mon instinct, je trouve que le plus petit triangle/parcours (EFD) est celui inscrit dans le cercle inscrit (encore une fois) dans le triangle/cellule (ABC).
(Appelons O le centre du cercle et I le milieu de [AC])
D'après la figure que je me suis faite : soit
On a aussi que :
et puisque : ,
et
Enfin, avec Pythagore dans BDO :
Application numérique : x=178.7 cm
Après tout.. C'est possible, non ?!



 bonjour a ts
bonjour a ts
jpense que c'est peut etre 208.4 cm
merci pour l'enigme
Bonjour à tous,
J'aurais bien voulu attendre notre ami Philoux pour stopper cette énigme car quelque chose me dit qu'il l'aurait appréciée. Son absence se prolongeant, je la cloture finalement.
Ce problème de géométrie m'a semblé intéressant pour une raison simple. En dépit du fait qu'une lourde résolution analytique existait, j'avais aimé le fait qu'une démonstration de niveau 4e était possible, en créant -comme certains l'on fait- les symétriques du point D par rapport aux côtés [AB] et [AC] du triangle. Les transformations sont souvent utiles dans les problèmes d'optimisation géométrique (distance minimale reliant un point A à un point B après passage sur une droite d ou problème du cheval qui a soif comme dit Meak, positionnement de 2 ponts sur des rivieres permettant de minimiser la distance...etc).
Ce problème m'a d'ailleurs permis -grâce à vos réponses- de (ré)apprendre la notion de triangle orthique (de ortho) ou triangle pédal (de pied). Merci de réactualiser mes connaissances en géométrie 
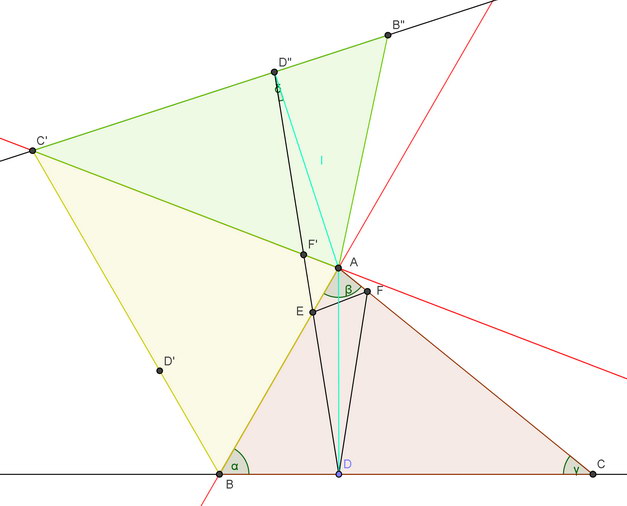
Pour expliquer brièvement cette démonstration, je me baserai sur la figure donnée par Manpower avec les symétriques D' et D''. C'est alors le segment [D'D''] qui donne le chemin le plus court.
Reste donc à déterminer la position de D sur [BC] pour que D'D'' soit minimale. Et ici point besoin de gros calculs.
En effet, on a (à cause des symétries) AD = AD' = AD''. Le triangle D'AD'' est donc isocèle en A et on montre facilement que l'angle aus sommet D'AD'' vaut 2 fois l'angle BAC soit 162°. Cette valeur ne sert à rien mais elle montre que cet angle est constant quelle que soit la position des points D' et D'' et donc du point D.
Par conséquent, pour que la base de D'AD'' soit minimale, il suffit que ses côtés le soient et par conséquent que AD soit minimale.
Cela est le cas lorsque D est le projeté orthogonal de A sur [BC] autrement dit le pied de la hauteur. CQFD
L'angle B mesurant 60°, on trouvait facilement X = 120 cm.
> Désolé Manpower, après avis du Conseil des Sages, il a été décidé que pour rester dans la lignée des précédentes applications du règlement des énigmes, ta réponse ne pouvait être acceptée, malgré ta démonstration correcte. Comme je dis souvent à mes élèves : vérifiez la plausibilité de vos résultats, et il faut avouer qu'être enfermé dans une cellule triangulaire de côté 2,4 centimètres à de quoi rendre fou  C'est souvent ce qui arrive lorsqu'on sort un exercice de son contexte pour le résoudre (habitude à faire de la géométrie en centimètres) et qu'on oublie de revenir à l'énoncé initial.
C'est souvent ce qui arrive lorsqu'on sort un exercice de son contexte pour le résoudre (habitude à faire de la géométrie en centimètres) et qu'on oublie de revenir à l'énoncé initial.
>Même remarque pour Prof2 : 1,2 m = 60 cm ? 
et aussi pour cinziani, réponse donnée en mètres au lieu de centimètres. Je suis un peu fautif sur ce coup car j'aurai dû vous laisser le choix de l'unité, je ne trouve pas très intéressant de piéger quelqu'un sur un problème de conversion et essaierai de l'éviter à l'avenir. (Hé oui moi aussi j'apprends au fur et à mesure les aléas du posteur d'énigme  ) Encore désolé.
) Encore désolé.
>Bigmaster, je trouve bien que tu essaies de participer aux énigmes de cette façon. Ici ta réponse me fait penser à mes élèves qui lorsqu'on leur demande une valeur en centimètres arrondie au millimètre ne savent rien faire d'autre que de donner la réponse en millimètres. Sache enfin que les énoncés sont rigoureusement contrôlés par un jury hautement qualifié  :D et que si une erruer intervenait elle serait corrigée avant. Au pire l'énigme serait annulée
:D et que si une erruer intervenait elle serait corrigée avant. Au pire l'énigme serait annulée 
>Torpedo, merci pour ta démonstration astucieuse et bien rédigée. Une lecture que je conseille à tous les mathimiliens 
>Gloubi, pas de souci car seul le résultat final compte. C'est logique car tu aurais pu comme d'autres poster un lacunaire et froid "120 cm".
A bientôt.
minkus
 Sacré Minkus, tu nous as bien eus avec tes trois étoiles !!! J'ai trouvé ton énigme avant d'aller me coucher, vers 1h du matin, et je me suis dit "une trois étoiles, je chercherai demain".
Sacré Minkus, tu nous as bien eus avec tes trois étoiles !!! J'ai trouvé ton énigme avant d'aller me coucher, vers 1h du matin, et je me suis dit "une trois étoiles, je chercherai demain".
Et puis j'ai regardé un peu, et ça m'a semblé si simple que je me suis demandée si c'était possible. Je n'ai même pas osé poster ma démo de peur d'âtre ridicule...
La voilà :
Effectivement on a affaire au triangle orthique et il suffisait de positionner le pied de la hauteur après avoir trouvé un angle de 60° par simple soustraction.
Ensuite, on avait un sinus de 0.5 et donc x = AB/2
Voili voilà. On ne devrait pas se fier au nombre d'étoiles 
Salut Borneo,
Je t'assure que je n'ai pas voulu vous pieger. Comme je l'ai dit j'avais oublie cette histoire de triangle orthique et pensais que l'astuce du symetrique n'etait pas vraiment evidente.
Cela dit, je me suis aussi dit que certains allaient choisir le pied de la hauteur par intuition sans etre sur d'avoir le minimum et j'ai donc hesiter a demander une demonstration.
Je me rends compte qu'il n'est pas évident de choisir le nombre d'étoiles. Par exemple, sans vouloir rien dévoiler sur une énigme en cours bien sûr  , certains , contrairement à toi si j'ai bien compris, ont trouvé le crypto 2 plus facile que le crypto 1. Après réflexion, je crois que j'aurais dû mettre une seule étoile aux deux car les prochains seront vriament plus durs et le nombre d'étoiles maxi est 4
, certains , contrairement à toi si j'ai bien compris, ont trouvé le crypto 2 plus facile que le crypto 1. Après réflexion, je crois que j'aurais dû mettre une seule étoile aux deux car les prochains seront vriament plus durs et le nombre d'étoiles maxi est 4 



 Concernant le débat sur le nombre d'étoiles :
Concernant le débat sur le nombre d'étoiles :
- J'ai cherché par intuition la solution... et je me suis planté... Cette énigme valait bien un 3 étoiles me semble-t-il, pour ceux qui n'avaient pas les connaissances nécessaires en géométrie (triangle orthoptique).
- entre crypto 2 et crypto 1, il est vrai que j'ai aussi trouvé plus facile crypto 2, grâce aux séparations des mots. Dans crypto 1 je n'avais pas vu l'astuce du décalage des 3 lettres et donc la recherche était plutôt coriace et valait un 4 étoiles ! Le "3 étoiles" de crypto 2 me parâit donc aussi justifié.



merci pour ces belles énigmes qui permettent de découvrir des notions ou de les réviser en s'amusant.
Je dois dire que le triangle orthique j'en avais jamais entendu parler ; pour la démo sans ses propriétes je dois dire que c'était effectivement pas de mon niveau!
J'ai aussi bien pu comprendre le principe de la contraposée avec le recto-verso, et bravo pour ton explication minkus parce que vraiment je comprenais pas. Après coup je me dis que c'était somme toute à ma portée si je m'étais concentrée !
 Aurelb, si je n'avais pas vu qu'il s'agissait du triangle orthique, voilà ce que j'aurais fait : sur une grande feuille de papier, j'aurais tracé le triangle à l'échelle, et fait quelques essais de tracé, et trouvé l'endroit qui donnait le trajet le plus court. En tâtonnant, j'aurais fini par trouver le pied de la hauteur.
Aurelb, si je n'avais pas vu qu'il s'agissait du triangle orthique, voilà ce que j'aurais fait : sur une grande feuille de papier, j'aurais tracé le triangle à l'échelle, et fait quelques essais de tracé, et trouvé l'endroit qui donnait le trajet le plus court. En tâtonnant, j'aurais fini par trouver le pied de la hauteur.
Bien sûr, il y a les logiciels de géométrie, mais ça demande plus de temps quand on ne sait pas très bien s'en servir. L'avantage de la géométrie, c'est qu'on peut mesurer et vérifier les réponses. 



certes, borneo. c'est juste que depuis le collège j'ai jamais vraiment aimé la geometrie et que j'ai pas mal oublié. Alors quand çà me semble insurmontable (parce que là il y avait la position de depart à trouver mais la distance changeait aussi en fonction des positions des autres points) je m'économise ! Tout est question de volontée en fait, c'est sur
 qqn peut il me dire à quel niveau ce fameux triangle orthique est abordé ?? Moi j'étais persuadé qu'il fallait utiliser les médianes pour faire cet exo ...
qqn peut il me dire à quel niveau ce fameux triangle orthique est abordé ?? Moi j'étais persuadé qu'il fallait utiliser les médianes pour faire cet exo ... 



 Bonjour,
Bonjour,
Suite à la remarque de Bornéo : j'avoue que j'ai bien essayé de dessiner quelques triangles sur un papier : par intuition, j'ai privilégié un (mauvais) choix de faire des triangles isocèles plutôt que de passer par les hauteurs. C'était assez séduisant. En tatonnant ... je me suis planté.
 Bonsoir,
Bonsoir,
> Manpower
"...:flagellation:..."
Tu es bien sur un forum SM mais ici, cela signifie "Sciences Maths"... 
Donc je doute que tu obtiennes satisfaction !!
A+, KiKo21.
D'ou as-tu sorti ca Borneo ? Ton lien ne fonctionne pas. Il va falloir que je revois les programmes Triangle orthique ? Quand je vais dire ca a mes 3e 
Cela dit, a ma decharge, je n'ai jamais eu de 4e et c'est la premiere fois cette annee. Et en voyant que la demo etait de niveau 4e, je me suis dit apres-coup que j'allais la donner a mes eleves. C'est parfait, je n'ai pas encore fait le chapitre sur "les droites remarquables du triangle".



 Bonjour,
Bonjour,
Merci Borneo.
Grâce à ton lien, je comprends mieux comment je suis passé à côté de la solution. En effet, comme tu l'as conseillé, il faut dessiner et faire quelques essais pour rechercher la bonne solution. Or dans ces cas là, on fait toujours des essais sur des cas extrêmes : j'avais bien cherché une solution avec les hauteurs, mais avec un triangle comprenant un angle obtu, je l'avais évidemment écarté. D'où la recherche d'une autre solution...
Question : quelle est le plus petit périmètre du triangle recherché, lorsque le triangle initial comporte un angle obtu ?
 Bonjour,
Bonjour,
Un triangle plat ??
Partant du sommet où l'angle est obtu (tu te cogne la tête sur 2 côtés en même temps) et allant sur le pied de la hauteur avec le côté opposé ??
C'est fou, non !?
A méditer...
A+, KiKo21.
 Bonsoir Bornéo,
Bonsoir Bornéo,
Je pourrais me joindre à vous ?
Moi aussi, je ne sais pas pourquoi mais je flaire l'arête prochainement...
Au fait, tu es bien en jaune et Manpower en violacé ??
Pour moi, je préfèrerai que tu t'arrêtes au rouge  !!!
!!!
Mes côtes vont mieux, je ne voudrais pas risquer la rechute...
A+, KiKo21.
Bornéo, dresseuse de bourrins
Nombre de participations : 0
Temps de réponse moyen : 39:52:24.

 )
)

