Inscription / Connexion Nouveau Sujet
différence entre axe/centre de symétrie d une courbe avec F
Bonjour, et oui je suis revenue! lol j'arrête.. Je voudrais savoir comment faire la différence entre axe et centre de symétrie si on me donne une fonction f (à partir de f sans dessin).
bonjour
as-tu entendu parler de fonctions paires ou impaires ?
Philoux
Oui fonction paire: f(x) = f(-x) [Axe] et impaire -f(x) = f(-x) [Centre]
Seulement le problème c'est que je vois comment incorporer ca dans la rédaction..
exemple: f(x) = (x+3)/(x-2)
Df = R - {2}
je sais pas si je peux mettre:
 x
x Df et puis la je fais comment..
Df et puis la je fais comment..
Le but est de réaliser un changement de repère dans lequel la fonction sera paire ou impaire
pour ton exemple, si tu fais un changement de repère pour lequel ta nouvelle origine est A(1,2) l'expression de Y=f(X) sera impaire et le point A sera un Centre de symétrie
Tu saisis ?
Philoux
lapsus calami : A(2,1) et non A(1,2)

Philoux
Oui je connais cette méthode c'est ce que j'ai trouvé o_U sans changement de repère.
f(x)=(x+3)/(x-2)
Df= R - {2}
donc a = 2
b = f(0) + (2a-x)
= 1
Sugestion: centre de symétrie de la courbe Cf de coordonnées (2,1) (le truc à montrer)
etc
en fait ta transformé la fonction paire en impaire O_U Je comprends pas.. Une courbe qui a un axe de symétrie (disons) a toujours un centre de symétrie quelque part aussi?
Non
Comme tu le vois sur ces courbes en exemple
Philoux
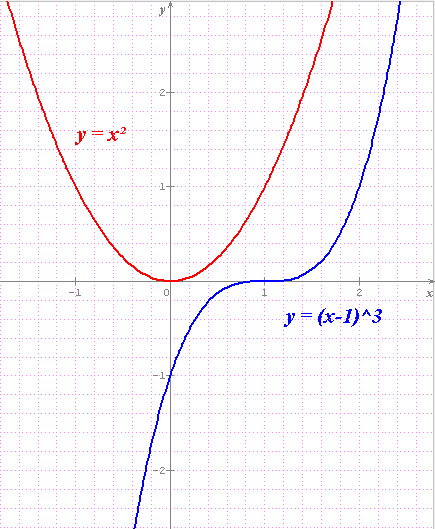
O_U mais tu as dit qu'il faut changer de repère afin de passer à une fonction paire à impaire... hm. Attends je viens de comprendre j'ai oublié qu'il y avait une modification à faire dans cette même fonction quand on change de repère.. Mais ca mavance pas.. J'aurai tjs une chance sur 2 aux devoirs..:/
j'ai oublié qu'il y avait une modification à faire dans cette même fonction quand on change de repère.. Mais ca mavance pas.. J'aurai tjs une chance sur 2 aux devoirs..:/
tu as dit qu'il faut changer de repère afin de passer à une fonction paire à impaire
Je ne crois pas avoir dit celà 
j'ai dit qu'une fonction ni paire ni impaire dans un certain repère pouvait le devenir dans un autre repère.
f(x)=(x+3)/(x-2) n'est ni paire ni impaire dans Oij mais devient impaire dans Aij
Bon courage
Philoux


