Inscription / Connexion Nouveau Sujet
DM maths fonctions polynômes de degré 2 avec graphique
Bonjour, j'ai un DM de maths à faire pour les vacances mais je ne sais pas comment le résoudre. Voici l'énoncé:
Le dessin de Gasper ci-contre est réalisé à partir d'arcs et de paraboles.
1. Proposer un repère pour cette figure.
2. Déterminer des fonctions polynômes de degré 2, définies chacune sur un intervalle, dont les courbes représentatives donnent une courbe croissante de - ; 0 et décroissante de 0;+
; 0 et décroissante de 0;+ .
.
Coup de pouce : Il est conseillé de choisir le repère de telle manière à ce que le haut de la tête de Gasper soit la représentation graphique de la fonction x  -x au carré +4 sur l'intervalle -2;2.
-x au carré +4 sur l'intervalle -2;2.
Pour obtenir les doigts de Gasper :
Soit f la fonction x  -k(x-a)(x-b)
-k(x-a)(x-b)
Calculer f(a) et f(b)
Donner le tableau de variation de la fonction f.
Montrer que f (a+b)/2 = k(b-a)au carré divisé par 4.
Merci beaucoup d'avance pour votre aide.
PS: désolé je ne suis pas arrivée à mettre le dessin de l'énoncé...
Bonjour,
le problème c'est que cet exo dépend essentiellement de cette figure
Tu dois donc d'abord redimensioner ta photo/scan à moins de 800x800 Pixels : ça doit tenir dans l'écran quand on force l'affichage "à l'échelle 1" (zoom = 100%, taille réelle des pixels)
Oui mais le souci c'est que je ne peux pas scanner... Et je ne peux pas faire de copier coller avec Word.
photographier un écran .. hum
de toute façon il y aura toujours avec une photo ou un scan le problème des dimensions en Pixels.
mais là pas besoin de photo !!
c'est à l'intérieur du document Word déja une image !
on peut donc extraire cette image nue de Word (clic droit dessus sans doute) et l'enregistrer (que l'image donc) dans un fichier à part (gif/png etc)
Au besoin on fait une copie d'écran (printscreen) et on la colle dans Paint
pour recadrer etc et sauvegarder sous format png ou gif.
J'avais un peu modifié la question 2 de l'énoncé pour que vous arriviez à imaginer à quoi ressemblait la courbe. Voici la question de l'énoncé :
2. Déterminer des fonctions polynômes de degré 2, définies chacune sur un intervalle, dont les courbes représentatives donnent le dessin proposé.
Voilà la courbe de l'énoncé, j'espère que vous arriverez à la voir.

Si c'est ça, bon courage !!
Il faut un très gros paquet de courbes du second degré pour faire ça !
rien que pour la "tête" il va à mon avis t'en falloir au moins 3 ou 4.
contrairement à ce qui est prétendu dans l'énoncé.
Tu peux simplifier (mais ça ne ressemble vraiment pas !)
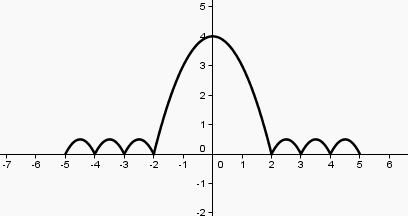
la "tête" est donnée dans l'énoncé (dans l'indice)
chaque doigt est aussi donné dans l'énoncé
pour diverses valeurs de a et b. k c'est à toi de le choisir (ça définit la "hauteur" du doigt)
ça te fait ici 7 fonctions du second degré, chacune définie (restreinte) dans un intervalle, ici les intervalles
[-5, -4], [-4, -3], [-3, -2], [-2, +2], [2, 3], [3, 4], [4, 5]
il faut remplacer a par x ?
a (et b et k) sont des paramètres, des valeurs numériques que tu dois choisir/déterminer.
quand on te dit "Calculer f(a) et f(b)" c'est remplacer x par a, puis par b.
ceci a pour but de te montrer comment déterminer a et b pour que la fonction -k(x - a)(x - b) passe par les points que tu veux.
Ah d'accord mais je croyais que b c'était y. Et on doit remplacer x par 2 ou -2 (on doit utiliser l'intervalle du doigt) ? Est-ce que pour calculer f(a) faut faire -k(x-a)? Pour a et x on prend 2 ou -2 aussi ? Merci d'avance.
on te suggère de calculer f(a) pour f(x) = -k(x-a)(x-b) où k, a et b sont des nombres dont la valeur exacte importe peu.
évidemment en remplaçant comme il se doit pour calculer f(a) x par a on obtient
f(a) = -k(a - a)(a - b) = 0 : a - a = 0, multiplié par n'importe quoi ça fait 0
cette suggestion a pour but de te faire vérifier que les valeurs de a et de b sont celles qui annulent f(x)
donc par exemple pour la tête, les valeurs qui annulent f(x) sont -2 et +2
la tête a donc pour équation -k(x + 2)(x + 2)
en choisissant k = 1 par exemple cela donne -(x² - 4) = -x² + 4 qui est la fonction "suggérée" pour cette tête !
a toi de faire de même pour chacun des doigts a et b sont les valeurs qui annulent la fonction donc les "bords" de chaque doigt, et k tu choisis et regardes ce que ça donne ...
 J'ai trouvé f(a) = 2 et f(b)=4. J'ai remplacé k par -1 voilà ce que ça donne:
J'ai trouvé f(a) = 2 et f(b)=4. J'ai remplacé k par -1 voilà ce que ça donne:
f(a) = -k(x-a)=0
-1(x-2)=0
-x+2=0
-x=-2
x=2
f(b)= -k(x-b)
= -1(x-4)
= -x+4= 0
-x=-4
x=4
Je sais pas après si faut faire comme ça, j'ai ensuite fait pour l'intervalle [2, 3]:
-k(x-a) (x-b)
= -k(2-3) (2-4)
= -1 (2-3) (2-4)
= -1(4-8-6+12)
= -16+14
= -2
Est-ce que c'est juste ? ESt-ce normal que je trouve ces résultats ?
f(a) = 2
Donc tes calculs, même pas regardé s'ils sont justes ou pas par ailleurs, n'ont tout simplement aucun sens.
f(a) = 0 et f(b) = 0 quels que soient a, b et k, et ce pour chacune des fonctions
Et je t'ai expliqué pourquoi :
a - a = 0, multiplié par n'importe quoi ça fait 0
tu as en tout 7 fonctions différentes à trouver, une dans chacun des intervalles cités précédement
Chacune de ces 7 fonctions correspond à une valeur de a, b, k précise qu'il s'agit donc de trouver. (donc 7 valeurs de a, 7 valeurs de b et 7 valeurs de k correspondantes)
je t'ai donné un exemple détaillé, complet et terminé, comment trouver la fonction dans [-2; +2] qui fait "la tête" de Casper,
et qui correspond à a = -2, b = +2 et k = 1
les inconnues la dedans ce n'est pas x, c'est a, b, et k.
on cherche "a" de sorte que pour x = -2 la fonction s'annule.
or la fonction s'annule pour x = a
donc a = -2
etc ...
j'ai ensuite fait pour l'intervalle [2, 3]: va pour cet intervalle
-k(x-a) (x-b) c'est quoi "ça" ???? f(x) = ...
pas juste "rien" suivi d'une expression reliée à rien.
= -k(2-3) (2-4) ????? calcul inutile qui ne rime à rien.
= -1 (2-3) (2-4) ??? pourquoi pas mettre k = 1, de toute façon comme l'expression elle même ne rime à rien (voir ci dessus)
= -1(4-8-6+12) et développer encore moins. si tu veux calculer cette expression, ça fait simplement et directement
-1 * (-1) * (-2) = -2
et tu en fais quoi de cette valeur -2 ??? rien du tout puisque tu ne sais même pas ce que tu as calculé (voir première ligne : tu écris une expression sans même savoir ce qu'elle représente ni pourquoi ni à quoi tu vas l'utiliser)
bref pour l'intervalle [2, 3] il s'agit de choisir a = 2 et b = 3 car la fonction doit s'annuler pour ces valeurs
et la fonction s'écrit f(x) = -k(x - 2)(x - 3)
point final.
Il reste maintenant non pas à calculer la valeur de cette fonction pour x = 2 ou pour n'importe quelle autre valeur de x mais à choisir k
et tu peux choisir pour k la valeur que tu veux :
cette valeur donnera la "hauteur" du doigt.
Si on voulait calculer la valeur de cette fonction pour une valeur particulière de x ce serait "au milieu du doigt" : le maximum.
C'est à dire pour x = (a+b)/2 = (2 + 3)/2 = 5/2 = 2.5 (pour ce doigt là)
seule valeur pour laquelle on peut avoir une raison de calculer f(x).
en effet :
f(2.5) = -k(2.5 - 2)(2.5 - 3) = -k(-0.5)(0.5) = 0.25 k
la hauteur du doigt est 0.25 k
tu choisis la hauteur du doigt
par exemple 0.5 cm et cela te donne 0.25 k = 0.5 donc k = 2
ou n'importe quelle valeur, comme tu choisis.
si tu veux un doigt de 1cm de haut tu choisis k = 4 etc ...
donc avec un doigt de 1cm de haut ta fonction dans [2, 3] sera f(x) = -4(x-2)(x-3)
tu peux la développer si ça te chante pour obtenir f(x) = -4x² + ...
tu fais pareil pour les autres doigts et chaque doigt a une valeur différente de a et b !!! (et éventuellement de k) et correspond à une fonction différente
Et au final la "fonction de Casper" est une fonction "définie par morceaux", comme on dit :
pour x dans ]-
 , -5[ la fonction n'est pas définie
, -5[ la fonction n'est pas définie
pour x dans [-5, -4] la fonction est f(x) = ...
pour x dans [-4, -3] la fonction est f(x) = ... une autre expression
etc ...
pour x dans [4, 5] la fonction est f(x) = ... encore une autre expression
pour x dans ]5, +
 [ la fonction n 'est pas définie
[ la fonction n 'est pas définie
les bornes des intervalles sont ouverts ou fermés au choix puisque aussi bien l'expression de l'intervalle de gauche que celle de l'intervalle de droite s'annulent toutes deux sur la borne commune aux deux intervalles.
Merci beaucoup pour ces explications et pour prendre du temps c'est très gentil, je crois que j'ai compris  ! Je suis désolée de vous obliger à développer vos explications mais j'ai des bonnes notes de partout sauf en maths...
! Je suis désolée de vous obliger à développer vos explications mais j'ai des bonnes notes de partout sauf en maths...
J'ai retrouvé avec la calculette x= 2,5 avec l'intervalle [2, 3] donc je vais essayer de me débrouiller pour les autres intervalles. Mais par contre, comment je vais faire pour trouver les autres expressions pour les intervalles [-4, -3],[4, 5] ?
J'ai retrouvé avec la calculette x= 2,5
que vient faire la calculette là dedans ? pour faire une addition de nombres entiers et une division par 2 tu as besoin d'une calculette ??
Pour les autres intervalles : pareil, les bornes des intervalles sont les valeurs respectives de a et b
(attention aux signes : "-a" avec a = -4, ça donne "+4")
Est-ce que vous pourriez m'aider pour l'intervalle [-4, -3] car je n'arrive pas à trouver k pour prouver que a+b/2 est bien égal à k(b-a)au carré /4. J'ai galéré à la calculette pour essayer de trouver ce nombre mais je n'y arrive pas. Pourriez-vous me dire comment faire pour trouver la bonne valeur de k s'il vous plait ? 
pour prouver que a+b/2 est bien égal à k(b-a)au carré /4
on a
et ça c'est valable toujours et ça n'a rien à voir avec la valeur de k.
ici on veut trouver k pour que
pour chaque doigt tu as (b-a)²/4 = 1/4 puisque on a pour chaque doigt |b-a| = 1 !
tu n'as pas besoin de calculette pour calculer ça !
pour l'intervalle [-4, -3] c'est a = -4 et b = -3, b - a = -3 -(-4) = -3 + 4 = 1, et ça donnerait pareil pour tous les autres doigts.
on a donc la hauteur du doigt = k/4, et ce quel que soit le doigt
et ça te donne la valeur de k sans calculette ni calculs "monstrueux" ! c'est instantanné !
c'est à toi de choisir la hauteur que tu veux et tu en déduis "instantanément" k en la multipliant par 4 !
(sans calculette).


