Inscription / Connexion Nouveau Sujet
droite parallèle et tangente
Bonjour,
Voilà je n'arrive pas à finir mon exercice de maths est ce que quelqu'un pourrait m'aider s'il vous plaît? c'est pour la question 3) a) et b).
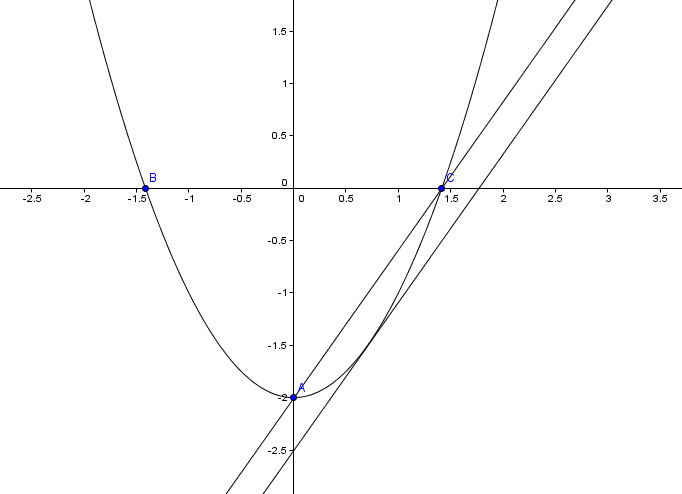
Dans le plan muni dans d'un repère orthonormé, la fonction f est représentée par la parabole P d'équation y = x²-2. Cette parabole coupe l'axe des ordonnées au point A et l'axe des abscisses en deux points B et C.
1) Déterminer une équation de la droite (AC).
2) la droite (AC)est-elle tangente à la courbe P?
3) a) Démontrer qu'il existe une unique droite parallèle à (AC) et tangente à P.
b) En donner une équation.
Mes réponses:
1) A(0;-2) B(-racine de 2;0) C(racine de 2;0)
y= racine de 2 x -2
2)Non, car elle coupe la parabole en deux point A et C or une tangente ne coupe jamais une parabole mais elle l'a frôle.
Et à partir de là je suis bloqué est ce qu'on pourrait m'aider svp?
PS: Normalement il y a un schéma de la parabole, de la droite (AC) et des points A,B,C
Bonjour
deux droites sont parallèles ssi elles ont même coefficient directeur
celui de (AC) est :
celui de la tangente à P en ,
OK pour 1) et 2) (pour 2) dit qu'une tangente ne coupe une parabole qu'en un seul point, ne dit pas qu'elle frôle qui n'est pas un terme très mathématique)
il faut maintenant que tu cherches une droite de coefficient directeur  2 tangente à la parabole.
2 tangente à la parabole.
une tangente en a, a pour équation y=f '(a)(x-a)+f(a) donc il faut que tu résolves f '(a)= 2 et tu trouveras a puis l'équation.
2 et tu trouveras a puis l'équation.
Oui cette propriété je la connais je me doutais qu'il fallait l'utiliser mais je ne sais pas comment.
Je me suis dit dit qu'il fallait faire avec la formule de l'équation d'une droite f'(x)(x-a)+f(x) mais le problème c'est qu'on ne connais ni a et ni f(x) donc je ne sais quelle formule utiliser
D'abord c'est y=f '(a)(x-a)+f(a) , tu connais tout, f(x)=x²-2 ; f '(x)=2x , a c'est ce que tu cherches.
D'accord donc c'est : racine de 2(x-a)+x²-2 mais y a toujours le problème du x parce que même si je résouds je ne peux pas avoir 2 inconnus et x sa peut pas être racine de 2 puisque c'est le coefficient directeur
mais je n'est pas ça moi j'ait f'(x) = racine de 2 comment est ce que vous avez fait pour trouver 2x ?
j'ai compris vous avez résolu racine de 2 x-2=0 mais ce que je ne comprends pas c'est que vous n'avez pas mis racine de 2 or pour que deux droite soit parallèle il faut qu'elle est le même coefficient directeur alors que vous vous mettez racine de 2 et 2 ce qui est différent
Le problème c'est que sa donne 2x(x-a)+x²-2 là on a deux inconnus x et a or on ne peut calculer 2 inconnus que par un système donc je ne sais pas à quoi correspond x est ce qu'on pourrait m'expliquer svp?
tu mélanges tout (les x de f '(x) et ceux de la droite) et tu ne lis pas les posts !
je répète : l'équation d'une tangente c'est y=f '(a)(x-a)+f(a) , tu connais tout, f(x)=x²-2 ; f '(x)=2x , a c'est ce que tu cherches.
donc f '(a) =  2 s'écrit 2a=
2 s'écrit 2a= 2
2  a=
a=  2 /2
2 /2
(c'est ce que t'a écris hekla d'ailleurs, il a juste appelé a x0.
Maintenant tu as trouvé a, tu peux écrire l'équation de la droite.
donc la réponse à la 3)a) c'est qu'il n'y a pas pas de droite tangente à la parabole et parallèle à (AC) puisque 2x(x-racine de 2/2)+x²-2 a un coefficient directeur différent de celui de la droite (AC) qui est racine de 2 c'est ça?
et pour la b) la réponse c'est 2x(x-racine de 2/2)+x²-2 ?



C'est bien ce que je me disais, tu ne lis vraiment pas les posts. non, tout ce que tu as écris est faux.
Je lis tout les post mais j'ai du mal à comprendre je ne vois pas ce qui est faux c'est pas sa l'équation de la droite parallèle à AC et tangente à la parabole?
parce que pour moi e lisant vos post c'est ce que vous avez dit
il y a un point où la tangente est parallèle à (AC) puisque l'équation admet une solution
l'abscisse du point est
D'accord merci là j'ai compris
Mais sinon pour la b) c'est bien 2x(x-racine de 2/2)+x²-2 la réponse?
je ne comprends pas f'(x) c'est 2x c'est ce que m'a mis glapion et donc sa veut dire qu'il faut que je remplace tous les x de 2x(x-racine de 2/2)+x²-2 par racine de 2 c'est ça?
f(racine de 2/2)=racine de 2/2 ²-2=-3/2
Donc ça fait racine de 2x(x-racine de 2/2)-3/2 c'est ça?
Mais les x on doit les laisser ou pas? parce que je ne sais pas à quoi sa correspond puisque sa peut pas être racine de 2 sur 2 puisque c'est a
ça y est j'ai trouvé! c'est égal à racine de 2(x-racine de 2/2) -3/2
mais il me reste toujours le x et je sais pas quoi en faire et à quoi il correspond est ce que vous pouvez m'expliquez à quoi il correspond s'il vous plaît?
donc pour trouver x je dois faire racine de 2(x-racine de 2/2)-3/2=0 c'est sa?
puis je trouve x=2+3racine de 2/4
ensuite est ce que je dois remplacer x dans 2(x-racine de 2/2) -3/2 ?
oui mais ça je l'ai déjà mis je veux savoir si je dois chercher à quoi correspond x et si une fois que je l'(ai trouvé je dois le remplacé dans racine de 2(x-racine de 2/2)-3/2
qu'est ce qu'une équation de droite ? c'est bien une relation entre l'abscisse et l'ordonnée d'un point
on vous a demandé l'équation d'une droite et rien d'autre à savoir
l'équation de la droite passant par et de coefficient directeur
ah d'accord c'est parce que je cherche l'équation d'une tangente c'est pour ça.
Donc la réponse c'est racine de 2x+racine de 2/2
puisque une équation de droite a pour formule ax+b c'est bien ça la réponse?
donc la réponse 3) b) c'est y=racine de 2-3/2
et pourquoi vous trouver -5/2 alors que moi j'ai -3/2?et même vous dans le post précédent vous avez mis -3/2
est la valeur de
pour
l'équation de la tangente est
en développant
d'où le résultat
graphiquement on voit bien que l'ordonnée à l'origine est -2,5
je comprends pas à coup vous me dites de ne pas utilisé la formule de l'équation de la tangente mais celle d'une droite puis maintenant je dis l'utiliser je ne comprends plus rien c'est laquelle que je dois utiliser?
je n'ai jamais dit qu'il ne fallait pas utiliser l'équation générale d'une tangente
18:08 c'est bien cette équation que j'ai écrite
de l'autre côté j'ai dit ce qu'était en général une droite et cette tangente en particulier
dans tous les cas vous obtenez comme équation
d'accord merci beaucoup là j'ai compris 
Et est ce que vous pouvez aussi m'aider sur un autre post que j'ai mis s'il vous plaît parce que personne ne me répond depuis tout à l'heure et je ne peux plus avancé. il s'appelle tangente, valeur graphique et nombre dérivé.
Et merci encore