Inscription / Connexion Nouveau Sujet
Exercice
Bonsoir je voudrais avoir des conseils pour un exercice la voici:
Exercice 110:QCM
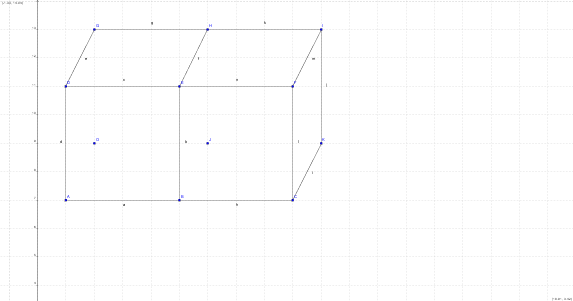
Deux cubes d'arête 1 sont disposés comme l'indique la figure ci dessous.L'espace est rapporté au repère orthonormé (O,OA,OJ,OG)
Pour chaque question,une seule réponse est exacte.Identifiez la.
Justifiez vos réponses.
1.Le triangle GIB est:
a/rectangle,b/équilatéral,c/isocèle.
2.Le point M tel que 2MO-MA+MC=0 est le point:
a/K,b/I,c/J
Une représentation paramétrique de la droite (KE) est:
a/x=t
y=2+t, t appartient à R
z=t
b/x=3+4t
y=t t appartient à R
z=4t
c/x=1-t
y=1+t t appartient à R
z=1-t
4.Le volume du tétraèdre DACH est:
a/1/2,b/1/6,c/1/3
5.La distance de C au plan (ADH) est:
a/2,b/1/2,c/
2.
Bonsoir,
en l'absence de la figure ou au moins d'une description précise et complète, il est absolument impossible de dire quoi que ce soit.
tu la scanne (que la figure) la photographie, ou la redessine avec un logiciel de dessin quelcomque (Geogebra, Paint, etc etc ...)
Si photo ou scan, tu passes obligatoirement le fichier sous Paintshop/Picasa etc ce que tu veux pour le ramener à des dimensions et qualité "pour le web" (maxi 800x800 pixels, définition en 72dpi maxi, qualité jpeg "simplement bonne")
une fois le fichier obtenu c'est là : 
[lien] dans la FAQ, avec usage du bouton "Img"
tu reduis la fenêtre même de geogebra pour que cette fenêtre ait une taille raisonnable (< 800x800)
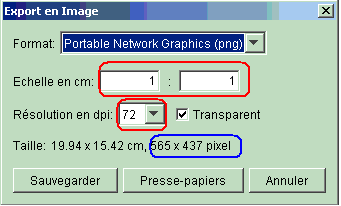
puis export en image png et tu vérifies que :
puis le fichier tu le joins ici avec le bouton Img
(la boite de dialogue et le bouton Attacher apparait un peu plus bas sur la page)
heureusement que j'avais pris les précautions d'écrire :
tu réduis la fenêtre même de geogebra pour que cette fenêtre ait une taille raisonnable
et tu vérifies que etc ...
donc tu réduis la fenêtre elle même de geogebra
et tu zoome/dézoome pour que ta figure tienne dans cette fenêtre réduite
et tu vérifie, bis répétita, que :
c'est à dire que l'échelle est bien 1 que les "dpi" sont à 72 environ
et que la taille en pixels est de l'ordre de 600x 500 environ.
sinon inutile, ton schéma sera illisible :
retour au point 1 : dimension de la fenêtre elle même etc.
La fenêtre de géogebra se réduit un peu et je n'arrive pas a la réduire totalement j'ai essayer de mettre l'image mais on vois encore rien pour l'export en image j'ai fais les réglages mais j'ai un problème pour réduire geogebra
la fenêtre de géogebra se réduit autant qu'on veut !!
une copie d'écran d'une fenêtre géogebra réduite à 581x348 pixels, boutons et tout compris :
et l'export correspondant :
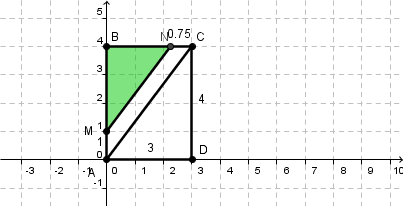
toutes mes images sont en taille réelles sans retouche ni reprises.
en particulier la taille de fenètre de geogebra est réellement telle que ma copie d'écran apparait en taille réelle.
m
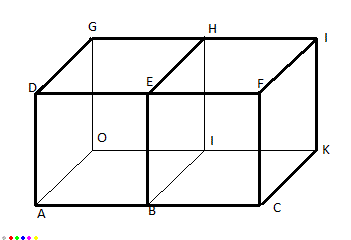
... mais si tu n'y arrives vraiment pas, tu fais ça avec Paint, tu mets les NOMS des points sur ce dessin là :
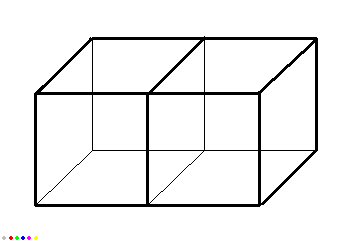
enregistrer l'image depuis le forum ("enregistrer sous")
edition dans Paint pour ajouter les noms des points
enregistrer le fichier
et attacher ici.
OK maintenant qu'on connait les points !
déja on place le repère :
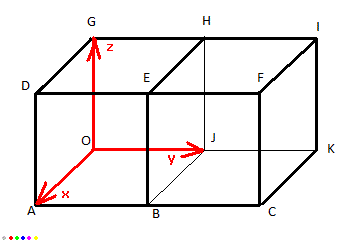
on peut alors au besoin obtenir les coordonnées de tous les points.
question 1
calculer les distances GI, GB, BI
la question 2 :
M tel que 2MO-MA+MC=0 ? (je suppose qu'il s'agit de vecteurs !)
ce point est le barycentre de (O,2) (A,-1) et (C,1) "par définition"
il appartient donc au plan OAC.
ses coordonnées sont obtenues par x = (2xO - xA + xC)/(2-1+1)
et y pareil (z = 0)
3) représentation de la droite KE
cette droite passe par K(0;2;0) et E(1;1;1)
chercher pour quelles valeurs de t on obtient un de ces points dans chaque cas.
4) volume d'un tétraèdre = (1/3) aire base x hauteur
choisir comme base DAC, la hauteur est alors évidente.
5) la distance de C au plan ADH consiste d'abord à identifier la perpendiculaire de C à ce plan (une droite simple à tracer)
S'il vous plaît je voudrais savoir les coordonnées de G,I et B pour pouvoir calculer les distances GI,GB,BI
Bonsoir,
je n'étais pas là pour poursuivre ...
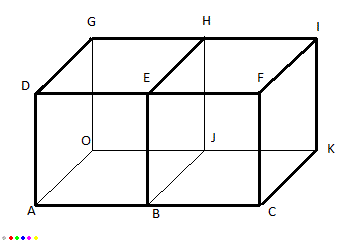
les coordonnées des points se lisent directement sur la figure du dernier post :
par exemple G(0;0;1) par définition même du repère utilisé : vecteur unitaire de l'axe des z !!
B(1;1;0) (x = 1, y = 1 dans le plan z = 0)
etc ...
tu en calcules la norme (la longueur)
norm d'un vecteur ||
|| = (X² + Y² + Z²)
ça te permet de vérifier avec Pythagore si oui ou non l'angle GBI est droit.
ou si deux ou trois de ces distances sont égales (isocèle/équilatéral)
nota : pour vérifier si GBI est droit on peut aussi calculer le produit scalaire si on sait le faire (c'est plus rapide que Pythagore) :
produit scalaire = 0 
vecteurs perpendiculaires ou au moins un des deux est nul
comme ici aucun n'est nul :
produit scalaire = 0 vecteurs perpendiculaire
1) visiblement faux car il est rigoureusement évident que BG = BI = 3 diagonale d'un cube !!!
pas le temps de chercher l'erreur.
2) une fois corrigé est-ce que BG² + BI² = GI² ?
c'est dans le plan (OJG) x = 0, sur la droite GI : z = 1
et sur la droite KI : y = 2
les coordonnées d'un point c'est (x;y;z) pas (x;z;y)
il est "visible" directement sans aucun calcul que BG et BI sont les diagonales des cubes, donc sont égaux et vallent
(1²+1²+1²) = 3
et que GI = 2 (deux fois l'arête des cubes)
le calcul est là pour t'habituer à faire ces calculs de coordonnées sans se tromper.
La lecture directe des longueurs "sans calculs" permet de t'autocorriger sans demander toutes les 5 minutes si l'unique ligne de calcul effectuée est bonne ou pas.
et que l'angle n'est pas un angle droit car effectivement
(
3)²+ (3)² 
la conclusion de la question 1 c'est :
le triangle est isocèle BG = BI, ni rectangle, ni équilatéral
Ceci dit essaye d'avancer un peu seul (je dois te quitter) sur les questions suivantes,
en t'autocorrigeant, par exemple en comparant des longueurs avec les valeurs "évidentes" lues directement sur la figure.
par exemple :
tu appelles x y z les coordonnées de M
tu écris les relations sur les coordonnées de M
par exemple
2(xO - x) - (xA - x) + (xC- x) = 0
avec xO, xA et xC les abscisses de O, A, C
et idem sur les ordonnées y et les "altitudes" z
tu en déduis x,y,z
tu cherches quel point a ses coordonnées là ...
(sinon de façon plus géométrique, mais qui ne fait pas l'objet de l'exercice; tu en déduis que M est un certain baryxcentre de O, A, C donc dans le plan (OAC) etc ... ce qui te permet de vérifier tes calculs)
La bonne réponse a la question 2 c'est le point J mais je ne sais pas le justifier vous pouvez m'aider ?
La justification c'est ce que j'ai déja dit :
tu appelles x y z les coordonnées de M
tu écris les relations
par exemple
2(xO - x) - (xA - x) + (xC- x) = 0
avec xO, xA et xC les abscisses de O, A, C
et idem sur les ordonnées y et les "altitudes" z
tu en déduis x,y,z
tu cherches quel point a ses coordonnées là ...
par exemple pour x :
tu as O(0;0;0), A(1;0;0), C(1;2;0)
donc 2(0-x) - (1 - x) + (1 - x) = 0
après simplification : -2x = 0, x = 0
(c'est bien l'abscisse de J !)
et pareil pour l'ordonnée y et pour z, tu les calcules de la mêm façon.
Annuler
connectez vous