- Bissectrice et cercle inscrit dans un triangle - Cours 4ème
- Exercice Bissectrices et cercles inscrits dans un triangle
- Cours sur les Figures planes, Distance d'un point à une droite et Tangente à un cercle
- QCM : Figures planes, distance et tangente - Exercice 4ème
- Six Exercices de géométrie pure - quatrième
Inscription / Connexion Nouveau Sujet
Exercice cosinus, cercle inscrit, angles, nature de triangles...
Bonsoir,
Je bloque sur un exercice... je vous le cite :
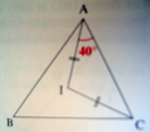
Le point I est le centre du cercle inscrit du triangle ABC.
1) Calculer la mesure des angles du triangle AIC et du triangle ABC.
En déduire la nature du triangle ABC.
2) La droite (BI) coupe (AC) en M.
Que peut-on dire de M ?
La figure ci-joint
Pour le point M je pense qu'il est le milieu du segment [AC] ...
Après pour calculer les anglais, je supose qu'il faut utilise le cosinus mais je ne vois pas trop comment...

Merci à vous !

Bonjour :
puisque I est le centre du celcle inscrit au triangle ABC, alors I est l'intersection des bissectrices du triangle .Donc...
oui c'est la droite du "milieu" de l'angle...
je sais pas si je m'exprime bien mais je sais se que c'est en tout cas...
Merci
Parfait !
Donc si (AI) est la bissectrice de l'angle ABC
alors l'angle BAI= l'angle IAC d'ou l'angle BAC=40+40=80°
On va commencer par chercher les angles du triangle AIC.
D'apres ton graphique AI=AC d'ou AIC est un ....
ok, ça m'avance déjà...
non ^^ AI n'est pas égal à AC
mais AI = IC...
Donc le triangle AIC est un triangle isocèle...
Donc l'angle BAC mesure 80°.... à cause de la bissectrice.. .
et comment je peux faire pour mesurer les angles des 2 triangles ?? 
Merci!
d'accord on a deja l'angle BAC=80°
Pour le triangle AIC isocele en I alors l'angle IAC=ICA=40°
or or tout les angles du triangle font 180° donc on peut trouver l'angle AIC . Tu sais comment faire ?
je sais le faire quand j'ai au minimum 2 angles sur 3 ou il suffit d'additionner et de soustraire mais là non je crois pas....
Merci à toi
ahhhhhhh j'avais pas pensé !
donc :
AIC = 180 - (IAC + ACI)
= 180 - 80
= 100°
L'angle AIC mesure 100°...
Reste à trouver l'angle ABC et ACB 
Merci !
On a finit avec le triangle AIC , maintenant ABC
on sait deja que (AI) et (IC) sont deux bissectrices d'ou l'angle BAC = 2* IAC
et l'angle ACB= 2* ICA
ah !
comme :
BAC = BAI + IAC
= 80°
ACB = BCI + ACI
= 80°
donc :
ABC = 180 - (BAC + ACB)
= 180 - 160
= 20°
l'angle ABC mesure donc 20°...
C'est ça ?
1) Nous sachons que l'angle IAC mesure 40°, et que comme les segments (AI) et (IC) sont égaux, en conséquent, c'est un triangle isocèle en I et que donc, ACI mesure aussi 40°, grâce à cela, nous pouvons en déduire que AIC mesure 100° grâce au calcul :
AIC = 180 - (IAC + ACI)
= 180 - 80
= 100°
Puisque I est le centre du cercle inscrit du triangle ABC, alors, [AI] et [IC] sont deux bissectrices du triangle ABC, et comme une bissectrice coupe langle en deux morceaux, il est logique que l'angle BAI soit égal à l'angle IAC, en conséquent :
BAC = BAI + IAC
= 40 + 40
= 80°
C'est la même chose pour les angles ICA et BCI, la somme des deux est de 80°
Nous sachons également que la somme des angles d'un triangle est égale à 180°, il suffit donc de faire :
ABC = 180 - (BAC + ACB)
= 180 - 160
= 20°
L'angle ABC mesure donc 20°
Le triangle ABC est lui aussi un triangle isocèle parce-qu'il à deux angles égaux et le troisième est différent...
2) Ce point M est le milieu du segment [AC] parce-qu'il passe pas le centre du cercle inscrit du triangle ABC en partant du point B.
Voilà, avec ça, le prof aura t-il quelque chose à reprocher ?
Merci !!
c'est bon pour la question 1- (je pense parce que je ne suis pas une prof )
)
mais pour la question 2 il ne suffit pas de dire que (BM) passe par le centre du cercle inscrit pour que ça coupe (AC) dans son milieu. Il faut le demontrer autrement. AS tu une idee ?
On a AIC un triangle isocele d'ou les mediatrices , les bissectrices les hauteurs et les medianes sont confondus .
Donc tu dois dire dans ta demonstration que la bissectrice (BI) est aussi une mediane et une meciatrice qui passe forcement par le milieu du cote oppose !
2) Ce point M est le milieu du segment [AC] parce-que la bissectrice (BI) est aussi une médiane et une médiatrice qui passe par le milieu opposé.
C'est bon ça ? (j'ai repris sur ton texte hein ^^) lol
Merci à toi !
il faut dire aussi que le triangle est isocele pour pouvoir dire que la bissectrice (BI) est aussi une médiane et une médiatrice .
Si non c'est parfait !
Lol mais je l'ai dit dans la dernière phrase du 1) ^^ mais sinon oui, je peux le rappeler...
Voilà ! enfin ce DM fini !
Merci beaucoup !


