Inscription / Connexion Nouveau Sujet
Fonction polynôme du troisième degré
Bonjour , j'ai un devoir maison en math pour demain et franchement je ne comprend rien du tout a l'exercice qui porte sur les fonctions polynôme du troisième degré.
Voici l'énoncé :
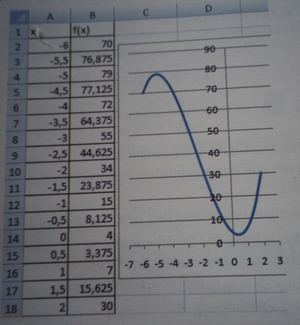
A l'aide d'un tableur , on a tracé la courbe représentative de la fonction f définie sur [-6;2] par f(x)= x³+7x²-5x+4.
1.Quelle formule a-t-on saisie dans la cellule B2 puis recopiée vers le bas , pour compléter la colonne B?
2.En utilisant les informations données par le tableur , faire une conjecture
sur le maximum et le minimum de f sur [-6;2].
3.Déterminer l'expression f'(x) en fonction de x.
4.Etudier le signe de f'(x) selon les valeurs de x , puis dresser le tableau de variation de la fonction f sur l'intervalle [-6;2].
5.Déduire de la question 4 , les valeurs exactes du maximum et du minimum de la fonction f sur l'intervalle [-6;2].
PS: Vous trouverez ci-joint le tableur
Je vous remercie d'avance , et je tiens a dire que si vous avez une des question , juste bien-sur , je prend !
Bjr
1.Quelle formule a-t-on saisie dans la cellule B2 puis recopiée vers le bas , pour compléter la colonne B?
Dans B2 sachant que dans la colonne A nous avons les valeurs de x, alors dans B2 nous avons = A2^3+7*A2^2-5*A2+4
essaie la suite, il n'y pas de grande difficulté
Merci pour ta réponse !!
Et pour la suite j'essaye mais j arrive pas , impossible a comprendre pour moi .
2.En utilisant les informations données par le tableur , faire une conjecture
sur le maximum et le minimum de f sur [-6;2].
quelle est la valeur maximale f(x) de cette fonction? En d'autre termes dans la colonne f(x), quelle est la valeur maximale de f(x)? pareil pour le minimum
Es tu sur que c'est pas la colonne x ?
on cherche le maximum de f(x) sur x variant de -6 à 2 alors
le maximum est 79 pour une valeur de x = -5
le minimum est 3,375 pour une valeur de x = 0,5
3.Déterminer l'expression f'(x) en fonction de x.
la dérivée d'une somme est la somme des dérivées
f(x)= x³+7x²-5x+4.
quelle est la dérivée de x3, de 7x² , de -5x et de 4 ?
La dérivée de x^3 c'est 3 ?
La dérivée de 7 x^2 c'est 9 ?
La dérivée de -5 x c'est 5 ?
Je comprend plus rien , la réponse de la 3 eme question c'est la fonction que tu as écrit ?
alors
la question 3 on demande de calculer f'(x) qui est la dérivée de f(x)
je pars donc de f(x) car c'est cette fonction que je dois dériver
ensuite je vois que f(x) est une somme de termes de degrés différents
f(x)= x³+7x²-5x+4
ca c'est la fonction de départ que tu dois dériver (moi je sais le faire, en premiere c'est indispensable de savoir faire ca, surtout qu'il n'y a aucune difficulté)
donc je vois que f(x) est une somme de termes, or je sais que la dérivée d'une somme est la somme des dérivées
donc tu dois calculer les dérivées de x3, de 7x² , de -5x et de 4 puis d'en faire la somme ce qui te permettra d'avoir la dérivée f'(x) de f(x)
tu dis:
La dérivée de x^3 c'est 3 ?
La dérivée de 7 x^2 c'est 9 ?
La dérivée de -5 x c'est 5 ?
les dérivées sont fausses. Pour t'aider, il faut connaitre les dérivées par coeur. On peut les retrouver dans un formulaire de dérivées à savoir
Tu peux en trouver ici:
dériver x3, utilise la dérivée de xn
la dérivée de 7x² est le produit de 7 par la dérivée de x². Dériver x² est la meme méthode que x3
la dérivée de -5x est le produit de -5 par la dérivée de x or comme la dérivée de x est 1 alors la dérivée de -5x est -5
dériver 4 revient à dériver une constante. Et la dérivée d'une constante = 0
Donc la dérivé de x^3 =3
La derivé de 7x²= 14
La dérivé de -5x=5
La dérivé de 4=0
Apres je fait 3+14+5= 22 et donc f'(x) = 22 ? C'est sa ?
la dérivée de x3
dans le formulaire la dérivée de xn est n*xn-1 donc ici n= 3 donc la dérivée de x3 est 3x²
la dérivée de f(x) est f'(x) = 3x²+14x-5
Ah mais c'est sa , mais je sais faire les dérivé alors , j'ai penser a sa mais je me suis dit que c'était hors sujet ! Et merci encore , et si tu pouvais me donner la réponse de la 4 et 5 merci !!!!
4.Etudier le signe de f'(x) selon les valeurs de x ,
f'(x) = 3x²+14x-5
il s'agit d'un polynôme du second degré, pour étudier le signe de f'(x) calcule les racines de ce polynome puis déduis en le signe de f'(x)
J'avais fait le même calcul j'ai du me tromper , merci de m'avoir corriger , je calcule vite les deux racines et je te dit sa
Ah oui effectivement j'avais fais 14^2 a chaque calcul , oui donc pour le deuxième je trouve , 0,3 ! Donc le signe de la fonction est positif ?
pas forcement, le signe de f'(x) indique le sens de variation de f(x). Quand tu regardes la représentation de fx), tu vois qu'elle est croissante puis décroissante puis croissante donc f'(x) est successivement positive, négative, puis positive
f'(x) = 3x²+14x-5
le signe de a est positif donc f'(x) est du signe de a donc positive à l'extérieur des racines et donc négative entre les racines racines
donc f'(x) > 0 si x  [-6;-5] et [1/3;2] et f'(x) < 0 si x
[-6;-5] et [1/3;2] et f'(x) < 0 si x  [-5;1/3]
[-5;1/3]
il faut déduire de la question 4, la réponse à la question 5
en fait dans la question 4 tu auras a calculer les images des points -5 et 1/3
donc calcule f(-5) et f(1/3)

 0 si x
0 si x  0 si x
0 si x 
