Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques SupérieurOn parle exclusivement de maths, pour le supérieur principalement, les BTS, IUT, prépas... Maths sup AnalyseTopics traitant de analyse [tout]Lister tous les topics de mathématiques
Niveau Maths sup
Partager :

Inégalité de Cauchy-Schwarz

Posté par
djstarmix 02-09-09 à 17:09

Voici l'énoncé :

Soient (xi)i[1,n] et (yi)i[1,n] deux familles de nombres réels.
Montrer que : [(k allant de 1 à n)(xkyk)]² + (1i<jn)[xiyj - xjyi]² = [(i allant de 1 à n)(xi)²][(i allant de 1 à n)(yi)²]

Si vous pouviez m'aider ce serait super Merci d'avance pour votre coopération !

Posté par
djstarmixDémonstration d'égalité difficile... 02-09-09 à 20:07

Bonjour...

Je suis en train de bien galérer sur la démonstration d'une égalité faisant intervenir des sommes et des carrés...

J'ai essayé beaucoup de moyens de résolution mais je ne suis pas bien éclairé... L'énoncé est en bas...

Merci d'avance pour votre coopération

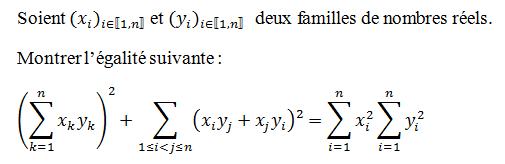
Démonstration d\'égalité difficile...

*** message déplacé ***

Posté par
Tom_Pascal Webmasterre : Inégalité de Cauchy-Schwarz 02-09-09 à 20:08

Bonjour,

attentionextrait de c_faq la FAQ du forum :

Q02 - Personne n'a répondu à ma question. Puis-je la reposter à nouveau ?



Merci.

Posté par
djstarmixre : Inégalité de Cauchy-Schwarz 02-09-09 à 20:10

Pardon... Y a une erreur... C'est :

Inégalité de Cauchy-Schwarz

Posté par
djstarmixre : Inégalité de Cauchy-Schwarz 02-09-09 à 20:10

Je pensais n'avoir pas été assez explicite

Posté par
soniagonre : Inégalité de Cauchy-Schwarz 02-09-09 à 20:42

Développe le 2ème terme, la double somme du truc au carré puis regroupe les termes que tu peux et si tout se passe bien tu devrais retomber sur les termes de ton égalité

Posté par
girdavre : Inégalité de Cauchy-Schwarz 02-09-09 à 21:20

Je crois que la récurrence marche (j'ai même fait le calcul!): on calcule la différence des termes avec les sommes jusqu'à n+1 et en la découpant (de 1 à n puis le terme correspondant à n+1) et en se servant de l'hypothèse de récurrence pour la première partie).
L'initialisation se fait facilement.

Posté par
djstarmixre : Inégalité de Cauchy-Schwarz 02-09-09 à 22:46

Mais on part d'où ?

Je veux dire... Pour l'hérédité, je calcule la différence des termes avec n+1 au lieu de n, j'isole les 1 à n des n+1 et je remplace grâce à l'égalité ?

Le problème, c'est que je n'arrive pas à développer le produit des deux sommes après le signe égal... Je n'arrive pas non plus à remplacer quoi que ce soit en fait...

Posté par
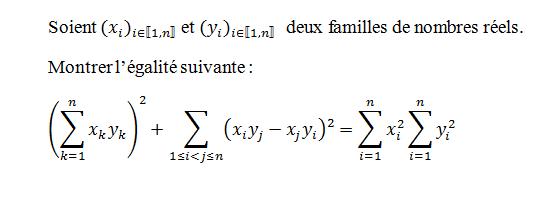
girdavre : Inégalité de Cauchy-Schwarz 03-09-09 à 09:39

Alors on a \(\Bigsum_{k=1}^{n+1}a_kb_k\)^2 + \Bigsum_{1\leq i<j\leq n+1}\(a_ib_j-a_jb_i\)^2 \\ = \(\Bigsum_{k=1}^na_kb_k +a_{n+1}b_{n+1}\)^2 +\Bigsum_{1\leq 1<j\leq n}\(a_ib_j-a_jb_i\)^2 +\Bigsum_{i=1}^n\(a_ib_{n+1}-a_{n+1}b_i\)^2
et \(\Bigsum_{k=1}^{n+1}a_k^2\)\(\Bigsum_{k=1}^{n+1}b_k^2\) = \(\(\Bigsum_{k=1}^na_k^2\)+a_{n+1}^2\)\(\(\Bigsum_{k=1}^nb_k^2\)+b_{n+1}^2\) \\ = \(\Bigsum_{k=1}^na_k^2\)\(\Bigsum_{k=1}^nb_k^2\) + b_{n+1}^2\Bigsum_{k=1}^na_k^2 +a_{n+1}^2\Bigsum_{k=1}^na_k^2 +a_{n+1}^2+b_{n+1}^2

Posté par
djstarmixre : Inégalité de Cauchy-Schwarz 03-09-09 à 17:58

Ah merci beaucoup Beaucoup, beaucoup, beaucoup !

Posté par
elhor_abdelali Correcteurre : Inégalité de Cauchy-Schwarz 03-09-09 à 20:40

Bonjour ;

ça se fait aussi directement :

4$\fbox{\Bigsum_{1\le i<j\le n}(x_iy_j-x_jy_i)^2=\frac{1}{2}\Bigsum_{1\le i,j\le n}(x_iy_j-x_jy_i)^2= \\ \frac{1}{2}\left(\Bigsum_{1\le i,j\le n}x_i^2y_j^2+x_j^2y_i^2-2x_iy_ix_jy_j\right)=\Bigsum_{i=1}^{n}x_i^2\Bigsum_{i=1}^{n}y_i^2-\left(\Bigsum_{i=1}^{n}x_iy_i\right)^2}

edit T_P : saut de ligne ajouté

Posté par
elhor_abdelali Correcteurre : Inégalité de Cauchy-Schwarz 04-09-09 à 02:53

Ah oui , c'est mieux comme ça ! Merci Tom_Pascal

Posté par
namlamre : Inégalité de Cauchy-Schwarz 05-09-09 à 17:35

A elhor_abdelali.

Bonjour, peux -tu m'expliquer d'où sort ton 1/2?? Et puis comment peux-tu faire disparaitre les j étant donné que i≠j??

Merci


Rechercher
Menu
Espace membre
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1674 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !