bonjour

peux-tu donner ton énoncé en entier ?

sinon, il faut déterminer les différentes valeurs de f(x) lorsque x varie de -8 à +8

et les valeurs extrêmes ( minimale et maximale ) de f(x) fourniront les bornes de l'intervalle dans lequel se situe f(x)

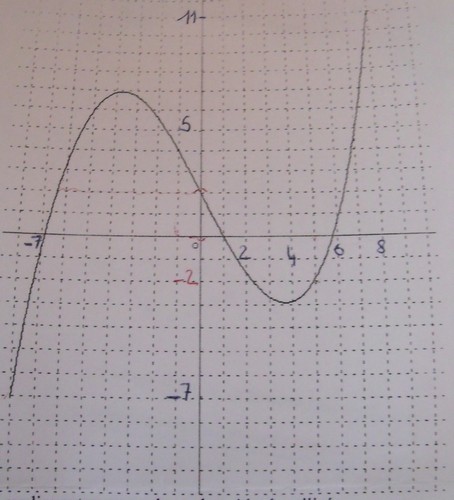
Lectures graphiques

1 - Quel est le domaine de définition de la fonction f ?

2- Donner f(-1) et f(-7)

3- Quelle est l'image de 5 par la fonction f? De 0?

4- Donner, s'il(s) existe(nt) les antécédents de -2 ; de 2 et de -9 par la fonction f.

5- Dans quel intervalle varie f(x) lorsque x varie dans [-8;8] ?

6a) Résoudre graphiquement l'équation f(x)=4 en expliquant la méthode utilisée. Puis résoudre l'équation f(x)=0.
b) Soit k un réel. Discuter, suivant les valeurs de k, le nombre de solutions de l'équation f(x) = k

7a) Résoudre graphiquement l'inéquation f(x)<2 en expliquant par une phrase la méthode utilisée.
b) Puis résoudre l'inéquation f(x)> 4

8 a) Indiquer les variations de la fonction f.
b ) donner le tableau de variations de f sur son domaine de définition.

9) préciser le maximum et le minimum de la fonction f.

10) Tracer la courbe représentative de la fonction g définie sur [-8;8] par g(x) = 1/2x + 2.

11) Résoudre l'inéquation f(x)>g(x).

voila

oui Agatheee

mais pour répondre aux premières questions, il faudrait avoir la courbe fournie

Oui je pense aussi.

Mais je comprends pas "dans quel intervalle varie f(x)"
Logiquement, si la courbe est tracé de [-8;8] alors x peut prendre toutes les
valeurs entre -8 et 8 ...

non, c'est x qui varie entre -8 et 8

tu as un scanner ? il est possible de joindre une figure grâce à [lien]

voila

eh bien voilà

tu constates que lorsque x varie de-8 à 8, f(x) évolue dans -7 à 11

tu es ok ?

Oui, mais c'est la même chose que d'écrire dans [-8;8] Non ?
Je vois pas la différence apart qu'on lit une fois sur les abcisses, et l'autre sur les ordonnées..

x [-8;8]

et

[b]f(x) [-7;11][/b]

x [-8;8]

et

f(x) [-7;11]

Ah d'accord. Je pensais que c'était une chose plus difficile que ça .

Merci

J'ai une autre question.

Pour la question 7 B

La rédaction est la suivante :

f(x) est supérieur ou égale a 4
On trace la droite d'inéquation y=4
On s'intéresse aux points de la courbe qui se trouvent au dessous ou sur cette droite les solutions sont les abcisses de ces points ... etc .


Est ce que l'on s'interesse aux points de la courbe qui se trouvent au dessous ou au dessus? J'arrive pas à comprendre comment l'on sait si c'est en dessous ou en dessus ?


Merci .

si on cherche f(x) >= 4 il faut des points de f tels que leur y soit supérieur à 4

donc il faut être AU-DESSUS de la droite y=4

aaaaaaaaaaaaaaaaaaaaaaaah oui ok merci !
:)