Inscription / Connexion Nouveau Sujet
nombres complexes
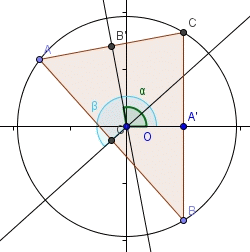
On a un triangle ABC quelconque avec les trois médiatrices D1 de [BC], D2 de [AC], D3 de [AB] et O le centre du cercle circonscrit au triangle (soit le point d'intersection des médiatrices). On a A', B', C', milieu de [BC], [AC], [AB]. On définit un repère où le vecteur OA'=u, (OA', OB')=alpha et (OA',OC')=béta. s1, s2, s3, réflexion d'axe D1, D2, D3. Comment définir les expressions complexes de s1, s2 et s3 ?
bonsoir et merci de me répondre,
j'ai copié directement l'exercixe demandé qui me cause souci n'ayant pas traité cette partie du programme.
o est le centre effectivement et le vecteur u doit être le vecteur unitaire mais cela n'a pas été précisé.
comment demarrer? je vais avoir du mal, je comprends peu de choses aux complexes.
merci pour l'aide
Les complexes sont un puissant outil de géométrie, en ce sens qu'ils permettent d'effectuer des calculs algébriques puissants qui sont l'exact réplique de propriétés géométriques.
Tu sais ce qu'est une réflexion d'axe Ox ?
tu sais ce qu'est un nombre complexe conjugué ?
Les deux notions sont identiques (on dit en maths de même forme - homomorphe )
Je reprends contact après une longue absence bien involontaire, veuillez m'excuser.
oui je vois bien sur le beau schéma réalisé ci dessus que cela donne.
s1 la reflexion d'axe D1 transforme B en C
s2 la reflexion d'axe D2 transforme c en A
s3 la reflexion d'axe D3 transforme A en B
comment passer aux expressions complexes de S1,S2,S3 ? en quoi le nombre complexe conjugué zbar = a-ib intervient-il?
un point M(x,y) est transformé en M'(x,y') avec y=-y'
cela signifie-t-il que OM = a+ib se trasforme en OM' = a-ib ? et ensuite comment intervienent les angles?
cela signifie-t-il que OM = a+ib se trasforme en OM' = a-ib
bien, et alors z se transforme en son conjugué.
réflexion d'axe Ox (donc d'axe (OA') :
Maintenant, pour celle d'axe OB', on va opérer comme ça :
je tourne la figure d'un angle
je fais la réflexion d'axe Ox (connue)
je tourne la figure d'un angle
Cela me fait faire la réflexion d'axe OB'
Connais-tu l'expression complexe d'une rotation de centre 0, d'angle
si je relis bien ce que vos remarquables cours proposent (je n'ai pas ceux complets de mon prof ayant subi une opération importante qui m'a fait perdre 3 mois et demi de cours) je lis:
z'-alpha = e^iteta(z-alpha) je ne sais ni ce que représente teta dans l'expression ni ce que signifie reellemnt cette formule mais je veux bien l'appliquer et comprendre la démarche que j'ai bien suivie jusque là.
merci
Soit M d'affixe z (cela veut dire que si les coordonnées de M sont (x;y) alors z=x+i*y)
Soit I un point fixe d'affixe
Soit un nombre réel
Soit r la rotation de centre I, d'angle
Soit M' d'affixe z' le transformé de M par cette rotation r
Alors z et z' vérifient la relation suivante :
Il ne suffit pas, hélas, de se contenter de réciter une formule, il faut aussi en comprendre les termes.
Donc là, on a une rotation de centre O, d'affixe 0, d'angle
Donc la relation devient
et la succession des transformations géométriques est en fait la composition des transformations complexes
rotation centre O, angle
réflexion d'axe Ox :
rotation centre O, angle
Il reste à recoller les morceaux pour trouver la relation entre et
On peut encore améliorer la formule, mais digère déjà ça.
merci,
il va me falloir un peu de temps pour faire le lien entre S1,S2,S3, et Z1,Z2,Z3 qui sont si j'ai bien tout suivi les expressions complexes des 3 reflexions. L'architecture est formidable pour aboutir au résultat.
remarquable ...j'ai encore beaucoup de retard à combler mais je crois qu'avec votre aide les choses iront de l'avant.
mille mercis et bonne fin de soirée.
Non, non :
j'ai seulement établi l'expression de la réflexion par rapport à OB'
Mais si ce n'est pas pressé, si ça peut attendre demain en soirée.
bonsoir dhalte,
je vais revenir un peu sur le pb commencé hier soir et dont la digestion est difficile.
je n'ai pas pu améliorer la formule de z3 qui me parait compliquée la reflexion s2 est difficile dans dans son écriture.
que dire alors de la reflexion s3?
il faut faire sans doute si j'ai bien compris une rotation d'angle -beta pour ramener oc' sur ox.
mais ensuite je ne saurai pas faire les reflexion s1 puis s2 et la rotation + beta pour trouver l'ecriture complexe de s3.
Je commernce à être dépassé par la composition des transformations complexes. Je pensais cela plus simple
La rotation de centre O d'angle -beta est:
z3 = ze^ -ibeta
reflexion d'axe ox : z3 = z2 bar
rotation o d'angle + beta :z4 = z3 eîbeta
mais ensuite pour trouver la relation entre z et z4 je me perds...Help
je ne suis pas sur du tout que tout ce qui précède soit juste. J'ai trop de retard pour rattraper tout cela...
ABC triangle quelconque
médiatrices D1 de [BC], D2 de [AC], D3 de [AB]
O centre du cercle circonscrit au triangle
A', B', C', milieux de [BC], [AC], [AB].
Repère centre O,
s1, s2, s3, réflexions d'axes D1, D2, D3.
Soit M de coordonnées (x;y) dans ce repère, d'affixe z=x+iy.
Soit M' le symétrique de M par rapport à D1, qui est l'axe des abscisses du repère.
Posons (x', y') coordonnées de M', donc d'affixe z'=x'+iy'
alors x'=x, y'=-y, c'est à dire x' + iy' = x - iy, c'est à dire
L'expression complexe de la réflexion d'axe D1 (c'est à dire celui des abscisses) est
Maintenant, on veut trouver l'expression complexe de la symétrie par rapport à la droite D2, qui fait l'angle
Pour cela, on décale la figure complète (A, B, C et M) en effectuant une rotation d'angle
Il faut simplement connaitre l'expression complexe d'une rotation de centre O (origine du repère), d'angle
donc on va suivre ce qui se passe pour M
rotation de M d'angle
symétrie de
et sachant que
rotation de
et sachant que
Voilà l'expression de la symétrie par rapport à D2
Évidemment, la symétrie par rapport à D3, qui fait un angle
Il suffit de remplacer
On pourrait s'arrêter là au vu de l'énoncé. Mais je suppose que ton exercice va un peu plus loin, et de toutes façons, ce qui suit te sera utile :
Maintenant, malgré ton retard, tu as au moins lu dans ton manuel de maths les trois propriétés suivantes (faciles à démontrer) :
Donc je reprends l'expression de la symétrie par rapport à D2
j'utilise
j'utilise
j'utilise
Interprétation : cette symétrie d'axe D2 est équivalente à la composition dans cet ordre d'une symétrie d'axe D1 (on calcule d'abord
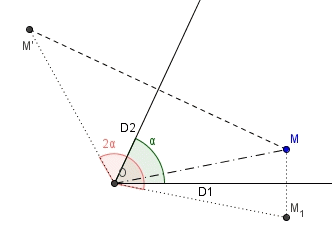
Cette figure te montre cette propriété :
pour passer de M à M' par la symétrie D2, on peut aussi passer d'abord par M1 par la symétrie D1, puis rejoindre M' par la rotation
Cet exercice doit te faire sentir (ferme les yeux et inspire un grand coup) toute la puissance de la représentation complexe des points du plan :
de simples manipulations algébriques (simples parce que le cours est assimilé, évidemment), permettent d'établir facilement d'importantes propriétés géométriques.
bonjour,
je te dis merci les yeux fermés.....et en soufflant un grand coup ,.ta démonstration est géniale, mais que de chemin à parcourir encore, il me faudra une autre année pour tout rattraper.
merci encore, et je te demanderai directement pour le prochain exo. celui la je le rendrai en retard, j'ai dit au prof que je n'arrivai pas au bout de la démonstration et que je me faisais aidé. C'est ce qu'il m'avait conseillé, mais je n'ai pas les moyens de payer des heures sup.
a+
mes camarades qui n'ont pas mon retard ont eu à la fin de leur exercice la question suivante:
si on fait: s3oS2oS1 quelle est la nature de la similitude?
est ce que cela signifie en regardant ton dessin que la figure n'a pas bougé?
tu n'es pas obligé de me répondre puisque ce n'était pas dans mon exo, mais si tu peux m'éclairer ce serait bien.
Merci
s3 o s2 o s1 veut dire qu'on applique d'abord la symétrie s1 par rapport à D1, puis ensuite s2 par rapport à D2, puis ensuite s3 par rapport à D3
s1 transforme en
tel que
s2 transforme en
tel que
s3 transforme en
tel que
s3 o s2 o s1 transforme en
il suffit de trouver la relation entre et
et de l'interpréter en termes géométriques.
Peux-tu la trouver ?
je crains le pire:
z3 =z2 e^2ibeta= (z1bar^ e2ialpha)bar.e^2ibeta = zbar e^-2ialpha.e2ibeta = ze^2i(alpha+beta)
je ne sais pas ce que cela signifie mais sans doute le plan reste-t-il dans sa position.?
L'effort est louable.
Le résultat ... peut être amélioré.
donc
Et tu peux vérifier que
donc
à part un conjugué qui manque et une erreur de signe, tu y étais presque.
Comment l'interprète-t-on ?
on part de z et on en prend le conjugué : symétrie par rapport à D1
et on multiplie le résultat par : rotation de centre O, d'angle
Donc s1 o s2 o s3 est la composée de s1 et d'une rotation.
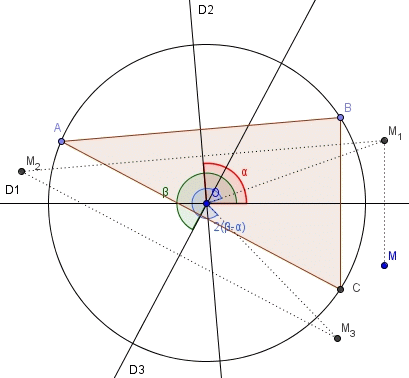
J'ai oublié de te signaler l'interprétation finale de la transformation s1 o s2 o s3
On a vu que son expression complexe était
Je t'ai dit que ça pouvait s'interpréter comme
symétrie par rapport axe des abscisses
suivi de rotation d'angle
mais cette expression est à rapprocher de celle qu'on avait obtenue pour s2
par analogie, s1 o s2 o s3 est une symétrie par rapport à la droite qui fait l'angle avec l'axe des abscisses.
Ci dessous une matérialisation de ce fait :
j'ai dessiné les transformations s1, s2 et s3 en pointillés noirs, pour faire passer M à M1 puis M2 puis M3.
j'ai porté en tirets rouges la droite d'angle avec l'axe des abscisses.
Et j'ai directement transformé M par la symétrie par rapport à cette droite (pointillé rouge)
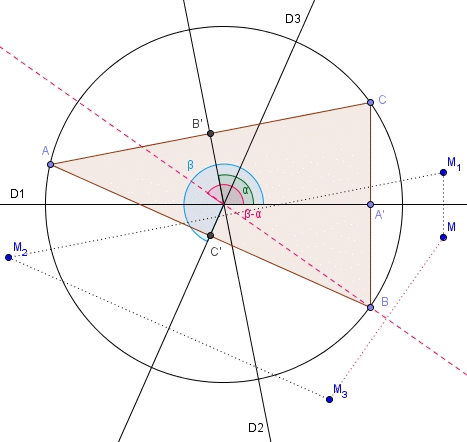
Cet axe de symétrie en tirets rouges passe par B
Sauras-tu le démontrer grâce aux nombres complexes ?