Pour la base c'est simple : tu traces un cercle de 2 cm de rayon.

Pour la partie latérale, tu dois calculer deux choses :

1- La longueur de la génératrice.
2- L'angle au sommet.

Pour la longueur de la génératrice AS? tu dois appliquer le théorème de Pythagore dans le triangle OAS rectangle en O.

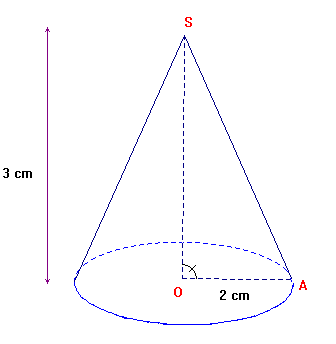
merci bocou mai je ne compren pas! cela nous donne une perspetiv. COmment j'obtien un patron?

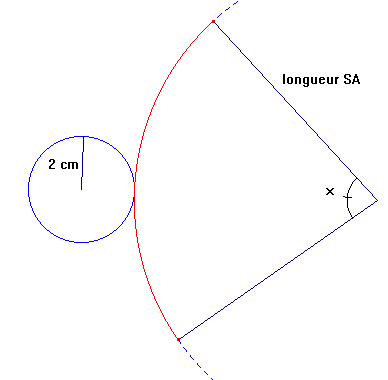
Une fois que tu connais SA, pour calculer l'angle x :

Il faut que périmètre du petit cercle = longueur de l'arc de cercle en rouge.

Périmètre du petit cercle = 2 2 = 4

Périmètre du grand cercle dont l'arc fait partie = 2 SA

Mais il ne faut en prendre qu'une partie, ses x/360 èmes (car ) (proportionnalité)

Donc longueur de l'arc = 2 SA

Ce qui te donne l'équation d'inconnue x :

2 2 = 2 SA

Tu peux diviser chaque membre par 2 puisque c'est un nombre différent de 0. Il te reste :

2 = SA

Ou encore 2360 = x SA

Ou encore x = 720/SA

En fait, on a : angle x = , ce qui  est logique car l'angle, par rapport à 360°, va avoir le même rapport de proportionnalité que le petit angle, par rapport aux 360° du petit cercle.

Je n'ai pas dit de bêtises ?

Ben je n'avais pas fini, je t'ai donné le problème par morceaux pour ne pas faire de trop gros messages. Regardre dans ton livre : il y a sans doute un exercice résolu qui peut te servir de modèle et te montre un exemple de parton de cône.

Merci bocou j vai essayé tou sa!

Pardon,je dois faire le patron d'un cone aussi de rayon 3 cm et de hauteur 4 cm et si possible avec des explication simple et detaillés S.V.P comme je ne comprend pas trés bien j'ai besoin d'aide voila
merci d'avance



PS:aussi est ce qu'on peut m'expliquer rapidement un volume du cone arondie au cm3 merci beaucoup

Enfin je suis entrain de faire le meme calcul mais je sais pas quel chiffre il faut remplacer^^

bonjour je dois faire moi aussi un patron et je voudrais suivre votre technique mais je ne comprend pas..c'est quoi Périmètre du petit cercle
Périmètre du grand cercle dont l'arc fait partie

Il a plus de trois ans ce topic... Ouh làlà...

Le périmètre du petit cercle est la longueur bleue, ici c'est 2 2 cm

Elle doit être égale à la longueur rouge (arc).

On connaît le rayon du grand cercle = la génératrice SA.
Donc le périmètre du grand cercle dont on voit l'arc rouge est 2 SA

On se demande donc quelle proportion de ce grand cercle on va prendre pour que la longueur rouge soit égale au périmètre bleu.

salu c pour vou demander si vou pourai maider la en faite c pour savoir comment on fai pour trcer le patron de la base dun cone merci davance

Avec une regle *******.

comment on fait pour savoit la taille de lange quand on veèut faire le parton ????