Inscription / Connexion Nouveau Sujet
"Points alignés"
Bonjours aux génies!
J'ai déjà beaucoup essayé...
Voici l'énoncé:
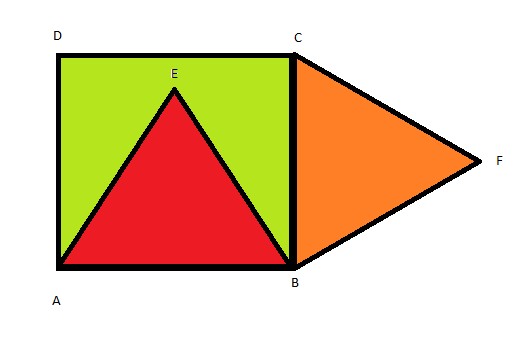
"Sur la figure suivante ABCD est un carré.
ABE et BCF sont deux triangles équilatéraux.
On se place dans le repère orthonormé (A,vecteur(AB), vecteur(AD)
1a. Démontrer que la hauteur des triangles équilatéraux est égale à racine(3)/2
b. En déduire les coordonnées des points E et F
2. Démontrer que les points D, E et F sont alignés."
Je sais que la "base" de la hauteur, notons la E', est 1/2 de AB. Et comme le segment [AB] est d'une part la base du triangle, et d'autre part la base du triangle, le côté du triangle doit avoir a même longueur que les côté du carré.
Je vous remercie en avance...
Salut
1)a. Moi je commencerai par introduire le point I milieu de [AB]. On se retrouve dans un triangle rectangle AEI ainsi on peu trouver la valeur de la hauteur. Comme ABE et CBF sont équilatéraux et de côté [AB] et [CB] ( ABCD étant un carré ) ils sont égaux donc la valeur de leur hauteur est la même.
b. Etant donné qu'on a maintenant la valeur de la hauteur on peut donc donner les coordonnée des point E et F dans le repère ( O , AB , AD )
2) Maintenant qu'on a les coordonnée des points A E et F on peut donner les vecteur AE et AF. Il faut donc montrer que AE = k AF k
 ( vecteurs collinéaires) et comme A appartient aux deux vecteurs les trois points sont donc alignés.
( vecteurs collinéaires) et comme A appartient aux deux vecteurs les trois points sont donc alignés.
Merci beaucoup!
Pour votre réponse à la question 1a. est-ce que je prend alors une valeur quelconque... car je ne connait aucune valeur... c'est cela qui m'embête un peu.
Je vous suis très reconnaissant de votre aide pour le reste.
Excusez moi j'ai trouvé la réponse... comme vecteur(AB) est un repère dans le plan, vecteur(AB)=1 non?
Bonjour, j'ai le même exercice à faire, mais je bloque sur les coordonnées de E pour pouvoir calculer IE..
Si quelqu'un pourrait me donner quelques indications!
Merci beaucoup !!
Bonjours lilounettec!
Tu es dans un repère ( A , AB , AD ). Donc AB = 1 et AD= 1.
AEB est un triangle équilatérale.
donc AE = AB = BE = 1
comme I milieu de AB, AI = 0.5
et maintenant tu utilise simplement le théo. de Pythagore; dans le triangle AEI.

Merci beaucoup pour votre aide!
Mais dans la question 2) pourquoi prendre le point A pour démontrer que les points D E F sont alignés ? On ne peut pas prouver qu'ils sont alignés en calculant les vecteurs DE et EF ?


