Niveau maths spé

Polynôme de Bernstein

Posté par
singe3 30-10-11 à 19:49

Bonjour

Je fais un exo sur les polynômes de Bernstein qui sont définis par :

Soit f une fonction de $[0,1]$ dans un Espace Vectoriel Normé E
Pour tout $n>0$ le n-ième polynôme de Bernstein de f est $B_{n,f}(x)=\sum_{k=0}^n f(\frac{k}{n})$ $n\choose k$ $x^k (1-x)^{n-k}$

J'ai répondu aux questions suivantes :

- Pour f(x)=1 sur $[0 ,1]$ , je trouve $\forall n>0$    $B_{n,f}(x)=1$

- Pour f(x)=x sur $[0 ,1]$ , je trouve $\forall n>0$    $B_{n,f}(x)=x$

Mais je n'arrive pas à trouver la question suivante :
Il faut démontrer que pour $f(x)=x^2$ on a $\forall n>0$    $B_{n,f}(x)=x^2(1-\frac{1}{n})+\frac{x}{n}$

J'ai essayé de plusieurs manières, changements d'indices, dérivation. Mais je bloque.

Quelqu'un peut m'aider ?

Merci

Posté par re : Polynôme de Bernstein 30-10-11 à 20:06

Pourtant la dérivation me semble bien (comme tu as fait pour x d'ailleurs)

Posté par re : Polynôme de Bernstein 30-10-11 à 20:12

salut,

Pour f(x)=x, j'ai d'abord remarqué que $f(\frac{k}{n})$ $n\choose k$ $=\frac{k}{n}$ $n\choose k$ $=$ $n-1\choose k-1$

Ensuite j'ai mis le x en facteur devant la somme dans l'expression de $B_{n,f}(x)$ et il apparait la formule de Newton on a $x(x+(1-x))^{n-1}=x$

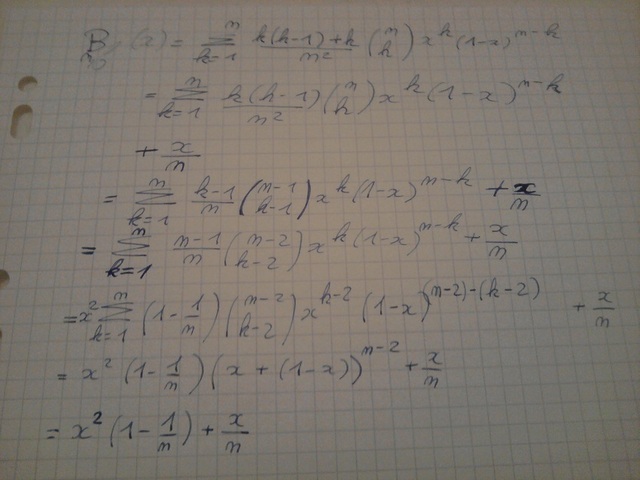
Posté par re : Polynôme de Bernstein 30-10-11 à 20:12

mais je n'ai pas dérivé pour f(x)=x

Posté par re : Polynôme de Bernstein 30-10-11 à 22:38

ok, mais on aurait pu , sinon $k^2 = (k(k-1) + k$ doit t'aider que tu dérives ou pas.

Posté par re : Polynôme de Bernstein 31-10-11 à 13:07

je n'y arrive pas non plus avec $k^2=k(k-1)+k$ , je tourne en rond et je retombe sur $B_{n,f}(x)=\sum_{k=1}^n\frac{k}{n}$ $n-1 \choose k-1$ $x^k(1-x)^{n-k}$ et je ne sais plus quoi faire

Posté par re : Polynôme de Bernstein 31-10-11 à 16:38

avec k(k-1) C(n,k) = n(n-1)C( n-2, k-2) tu devrais t'en sortir.

Posté par re : Polynôme de Bernstein 31-10-11 à 19:43

Salut

Grâce à ta dernière indication je crois avoir trouvé.
Pour le terme x/n apparaissant dés la 2eme ligne j'ai utilisé le résultat pour f(x)=x pour aller plus vite
Comme c'est assez long à taper en latex je l'ai pris en photo.
C'est correct ?

Polynôme de Bernstein

Merci

Ce topic

Imprimer
Réduire / Agrandir
Pour plus d'options, connectez vous !
Fiches de maths

analyse en post-bac
21 fiches de mathématiques sur "analyse" en post-bac disponibles.

Rechercher

Espace membre

Zone membre

Pas de compte ?
Je m'inscris

Changer d'île

Cours et Exercices de maths

Forum de maths

college

lycee

Outils de maths

Pages les plus populaires

Polynôme de Bernstein

Seuls les membres peuvent poster sur le forum !

Ce topic

Fiches de maths