Inscription / Connexion Nouveau Sujet
Position relative de deux courbes
Bonjour,
J'aurai besoin de votre aide sur un exercice de fonction :
Soit x un nombre réel strictement positif
1. Comparer x et 1/x sur l'intervalle ]0;- [
[
Donc là j'ai fait: Soit x > 0
x et 1/x  ]0;-
]0;- [
[
tel que 1/x < x
2.En déduire la position relative des courbes représentatives des fonctions f et g telles que f(x)=x et g(x)=1/x en fonction de x.
Donc là je suis partie comme ça: Soit f et g définie sur ]0;- [
[
x, 1/x  ]0;-
]0;- [ tel que 1/x < x
[ tel que 1/x < x
f(x)-g(x) = x - 1/x
Mais je bloque :S Il faut que je trouve si f(x)-g(x) est soit positif soit négatif, pour en déduire si la fonction f(x) est eu dessus, ou en dessous de la fonction g(x) mais je bloque avec le calcule >.<
Merci d'avance pour votre aide,
Toffu.
Bonjour Tofu,
Humm .... je ne suis pas convaincu que tu aies pris cet exo dans le bon sens, si je peux me permettre .
Léo
Bonjour,
attention à l'écriture de l'intervalle...
puisque x > 0 il s'agit de ]0;+ [...
[...
Donc là j'ai fait: Soit x > 0
x et 1/x ]0;+
 [
[
tel que 1/x < x
tu n'as strictement rien démontré......
pour comparer x et 1/x tu dois calculer la différence
comme x>0 cela revient à étudier le signe de (x - 1)....
Oups je suis vraiment désolé, c'était l'intervalle : ]0; + [
[
Merci de votre aide,
donc ca me donne : x+1 =0 ou x-1 =0
 x=-1 et x= 1
x=-1 et x= 1
d'où x>0 donc x=1
et après je compare ?
(Hum...je suis pas sure d'avoir tout compris >.<)
pour comparer x et 1/x
1) tu calcules la différence x - 1/x : c'est fait
2) tu étudie le signe de cette différence
tu as
tu pourrais faire un tableau de signes, mais ici il est plus simple de remarquer que :
puisque x > 0, alors (x + 1) est aussi positif et que le signe de
dépend uniquement du signe du facteur (x - 1) (règle des signes...)
Si (x - 1) est positif, c'est à dire x - 1 > 0, alors car tous les facteurs ont positifs
Si (x-1) est négatif, c'est à dire x - 1 < 0, alors car, sur les 3 facteurs, un seul est négatif
reste à savoir quand x-1 est positif ou négatif....
pour le savoir,il suffit de résoudre l'inéquation
x - 1 > 0
x > 1
en conclusion
Lorsque x > 1 alors (x - 1) > 0 donc et x > 1/x
font color=blue>
Lorsque x < 1 alors (x - 1) < 0 donc et x < 1/x
..clic trop rapide 

Lorsque x < 1 alors (x - 1) < 0 donc et x < 1/x
maintenant tu peux en déduire la position des deux courbes
Merci beaucoup pour votre aide! J'ai beaucoup mieux compris. ^^
Donc j'en déduis que étant donné que f(x)-g(x) >0 ( vu que ca revient à (x-1)(x+1)/x >0)
que pour tout x réel de ]0;+ [ la fonction f est strictement au dessus de la courbe g.
[ la fonction f est strictement au dessus de la courbe g.
Merci merci beaucoup!!
Bonne journée,
Toffu.
Donc j'en déduis que étant donné que f(x)-g(x) >0 ( vu que ca revient à (x-1)(x+1)/x >0)
que pour tout x réel de ]0;+[ la fonction f est strictement au dessus de la courbe g.
non, c'est inexact, tu n'as pas bien lu ce que je t'ai écrit......
relis mes posts
tu as deux cas à envisager :
1er cas : x < 1
et
2nd cas : x > 1
Oh...
Mais quand on résout l'inéquation x-1> 0 et qu'on trouve x > 1 on a encore besoin de d'envisager les deux cas ? ^o)
j'aurais dû préciser : tu as deux cas à envisager lorsque tu conclus
x ]0;+
]0;+ [
[
il faut donc voir quelle est la position des courbes quand x < 1
puis quelle est la position des courbes quand x >1
pour avoir une idée,sur ta calculatrice graphique, trace sur un même écran les deux courbes lorsque x > 0 tu verras ainsi laquelle est au dessus de l'autre et pour quelles valeurs de x...
tu peux aussi utiliser Geogebra pour tracer les deux courbes...
Mmmh...je suis un peu perdue :S Dans notre cours le prof était partie sur un simple calcul, je pensais pas que c'était aussi complexe >.< Enfin les fonctions et moi c'est pas vraiment ça aussi :S
Je comprend pas pourquoi le résultat de l'inéquation ne nous sert pas vraiment ?
encore une fois tu n'as pas bien lu ce que je t'ai écrit....
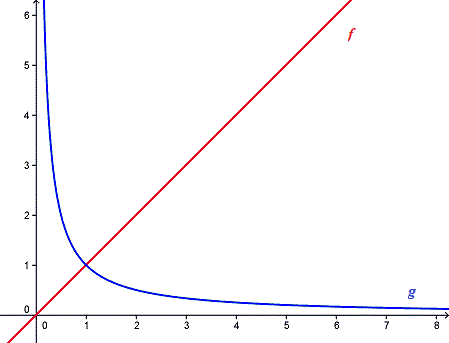
quand 0 < x < 1 alors x - 1/x < 0 donc x < 1/x ce qui signifie que la courbe représentant f est au dessous de celle représentant g
quand x > 1 alors x - 1/x > 0 donc x < 1/x ce qui signifie que la courbe représentant f est au dessus de celle représentant g
quand x = 1 x - 1/x = 0 cela signifie que la courbe représentant f coupe celle représentant g
je te joins le graphique : en rouge la courbe représentant f et en bleu la courbe représentant g....
Ah d'accord!! Je pensais qu'il suffisait de démontrer qu'un seul cas, je pensais pas qu'il fallait faire les 3 cas, lorsqu'il est négatif, positif, et égale.
Là c'est bon je pense avoir bien compris! Je vais m'occuper de bien tout présenter et de tout bien relire aussi 
En tout cas merci beaucoup d'avoir pris de votre temps pour m'aider!
Bonne soirée,
Toffu.




