Niveau autre

Proba : combinaisons de 5 dés sur un seul lancer de 15 dés

Posté par
Myssee 24-10-13 à 17:28

Bonjour à tous,

je suis créateur de jeux de société amateur, ai arrêté les maths au bac ES il y a plusieurs années, et ai besoin de vos lumières sur un problème de dés.

Un joueur lance 15 dés simultanément. Tous les dés sont identiques, marqués sur chacune des faces d'une couleur distincte (6 faces : rouge, bleue, jaune, verte, mauve, noire).
Le but est d'accomplir une combinaison sur 5 dés parmi ces 15. Par exemple : au moins 5 rouges ; au moins 4 rouges et 1 jaune ; au moins 3 rouges, 1 jaune, 1 bleu ; etc.
Je vous passe le système de jeu avec des relances de dés par chaque joueur dans le pool commun.

J'ai bien déterré le schéma de Bernouilli, qui fonctionne pour "au moins 5 rouges" (8,98% de chance sur 1 lancer), je l'ai appliqué pour les autres combinaisons en considérant les événements indépendants (ex. au moins 3 rouges et 2 jaunes : 46,78% * 74,04% = 34,64% de chance sur 1 lancer), mais je sais qu'ils ne sont pas indépendants (le calcul précédent contient "tous les dés sont rouges" et "tous les dés sont jaunes")

Donc, vous voyez où je veux en venir : comment calculer les probas des combinaisons dépendantes, vu que je ne sais pas à quel point les événements sont justement dépendant ?

Je cherche la formule qui m'aidera à définir, pour mon jeu, le nombre de dés dans le pool (10, 15, 20) et les tailles et "formes" optimales des combinaisons (avec des niveaux de difficulté).

Merci de vous pencher sur mon problème, et désolé si mon énoncé est peu clair, mon niveau en math est limité.

Posté par re : Proba : combinaisons de 5 dés sur un seul lancer de 15 dés 24-10-13 à 18:13

salut

oui c'est bernoulli

P( au moins 5 rouges sur les 15 lancés )= 1- [P(0 rouge) + P(1 rouge) +..+P(4 rouges)]

la proba elementaire avoir 1 rouge  sur un dé = 1/6

P( 0 rouge)= C15,0*(1/6)^0*(5/6)^15

P(1 rouge )= C15,1*(1/6)*(5/6)^14

P(2 rouges)= C15,2 *(1/6)²*(5/6)^13

P(3 rouges)= C15,3*(1/6)^3*(5/6)^12

P(4 rouges)= C15,4*(1/6)^4*(5/6)^11

et donc P( au moins 5 rouges )= 1 - C15,0*(1/6)^0*(5/6)^15 - C15,1*(1/6)*(5/6)^14 - C15,2 *(1/6)²*(5/6)^13 -

C15,3*(1/6)^3*(5/6)^12 -  C15,4*(1/6)^4*(5/6)^11.

Posté par re : Proba : combinaisons de 5 dés sur un seul lancer de 15 dés 24-10-13 à 18:16

pour au moins 4 rouges

P( au moins 4 rouges sur les 15 lancés )= 1- [P(0 rouge) + P(1 rouge) +..+P(3 rouges)]

avec la meme facon de calculer que precedement (P(X=k)= C15,k*(1/6)^k*(5/6)^(15-k)) pour k compris entre 0 et 3.

Posté par re : Proba : combinaisons de 5 dés sur un seul lancer de 15 dés 24-10-13 à 22:33

Merci flight pour tes réponses.

J'ai bien trouvé la méthode, suivant le schéma de bernouilli, pour connaître la proba d'avoir 5 rouges sur les 15 dès (ou 4...)

Ca se corse lorsque je veux connaître la proba d'obtenir une combinaison telle que :
"au moins 3 dés rouges, 1 dé jaune et 1 dé bleu".

Je sais le faire si je considère les événements indépendants :
P(combinaison) = P(rouge>2)*P(jaune>0)*P(bleu>0)
Mais je sais que ça cloche, car les événements ont une certaine dépendance :
ce calcul fonctionne pour 3 lancers de 15 dés séparés, alors que la combinaison doit être effectuée sur le même lancer.

Peut-être que je raisonne mal sur ce coup, ou peut-être que la dépendance est marginale.
Je cherche une formule me permettant de calculer les probas de toutes les combinaisons de dés/couleurs, sachant que je veux pouvoir faire varier et le nombre de combinaisons (5,4,6 ou +) et le nombre de dés à lancers (15,mais peut-être 20).
Je cherche des combinaisons viables (pas de probas infimes) et avec plusieurs niveaux de difficulté pour équilibrer mon système de jeu.

Posté par re : Proba : combinaisons de 5 dés sur un seul lancer de 15 dés 25-10-13 à 16:24

Bonjour Myssee,

On peut schématiquement "comprendre" la loi binomiale comme suit :
On réalise n tirages identiques ayant deux issues possibles :
issue de type 1,  de probabilité p1
issue de type 2,  de probabilité complémentaire p2 = 1 - p1
On s'intéresse aux variables aléatoires N1 et N2 (N1 + N2 = n) :
N1 nombre d'issues de type 1
N2 nombre d'issues de type 2

Pour obtenir UN tirage particulier ayant N1=n1 et N2=n2 :
... il faut tirer n1 fois avec une probabilité p1 et n2 fois avec une probabilité p2...
...ce qui fait donc une probabilité élémentaire de $p_1^{n_1}.p_2^{n_2}$

Il faut ensuite multiplier cette probabilité élémentaire par le nombre de façons d'obtenir cette répartition n1 et n2 :
Il y a en tout n! permutations possibles des n lancers.
Mais comme n1! permutations des tirages de type 1 et n2! permutations des tirages de type 2 ...
... laissent la combinaison obtenue inchangée, le nombre de combinaisons   $n_1 + n_2 = n$   sera de   $\dfrac {n!}{n_1!n_2!}$
$\implies \boxed {  p(N_1=n_1, N_2=n_2) = \dfrac {n!}{n_1!n_2!}.p_1^{n_1}.p_2^{n_2}  }$

Ce qui redonne bien la formule de la loi binomiale (en considérant N1 = X = succès, p=p1 et q=p2=1-p)...

On peut généraliser à ce qu'on appelle la loi multinomiale :
On réalise n tirages identiques (par exemple n=15 dés) ayant m issues possibles (par exemple m=6 faces) :
issue de type 1,  de probabilité $p_1$
issue de type 2,  de probabilité $p_2$
...
issue de type m,  de probabilité $p_m$

$p_1 + p_2 + ... + p_m = 1$

On s'intéresse aux variables aléatoires $N_1, N_2, ... N_m$ :
$N_1$ nombre d'issues de type 1
$N_2$ nombre d'issues de type 2
...
$N_m$ nombre d'issues de type m

$N_1 + N_2 + ... + N_m = n$

De façon similaire à la loi binomiale, on obtient la loi multinomiale :

$\implies \boxed {  p(N_1=n_1, N_2=n_2, ..., N_m=n_m) = \dfrac {n!}{n_1!n_2!...n_m!}.p_1^{n_1}.p_2^{n_2}....p_m^{n_m}  }$

Avec cette formule, tu peux donc modéliser aussi finement que tu le veux la dynamique de ton jeu.
Tu écris chaque "règle" sous la forme d'une condition précise.
Puis tu sommes les probabilités de chaque éventualité répondant à cette condition, en utilisant correctement les indices.
Cela peut se faire par programme, ou peut-être plus facilement sur tableur...

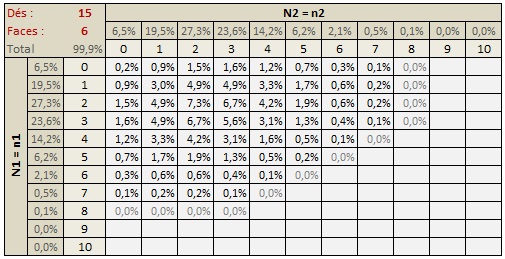
Exemple... P(4 rouges et 2 jaunes) pour 15 dés :
n = 15
p1 = p2 = 1/6
p3 = 4/6  (toute autre face que "1" et "2")

$p(N_1=4, N_2=2, N_3=9) = \dfrac {15!}{4!.2!.9!}.(\frac 1 6)^4.(\frac 1 6)^2.(\frac 4 6)^9$

Posté par re : Proba : combinaisons de 5 dés sur un seul lancer de 15 dés 25-10-13 à 18:20

$P(N_1 = n_1 ; N_2 = n_2)$

Proba : combinaisons de 5 dés sur un seul lancer de 15 dés

$P(N_1 \ge n_1 ; N_2 \ge n_2)$

Posté par re : Proba : combinaisons de 5 dés sur un seul lancer de 15 dés 25-10-13 à 18:22

Et si le jeu est un succès je veux des pépettes ...

Posté par re : Proba : combinaisons de 5 dés sur un seul lancer de 15 dés 26-10-13 à 03:47

Merci beaucoup LeDino !

Clair, net, précis, pédagogique, avec exemple à l'appui, c'est parfait.
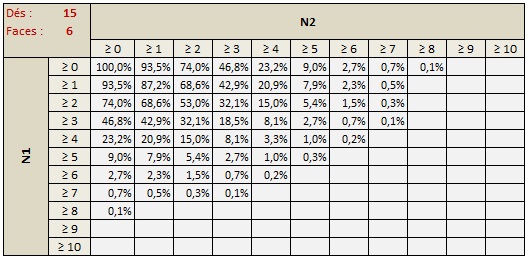
J'ai dû un peu me creuser pour comprendre, mais les tableaux et quelques essais m'ont permis d'assimiler cette loi multinomiale.

Reste à mettre tout cela en forme sous tableur, surtout pour des combinaisons comportant plus de 2 couleurs. Ca oblige à additionner de nombreuses possibilités, mais c'est faisable, car avec les arbres j'étais bloqué.

Les probas, pour la création de jeux, ça écrème de nombreux tests inutiles, et des outils comme celui-ci peuvent ouvrir sur de nouvelles idées !

Ensuite, pour le succès, c'est autre chose...

Ce topic

Imprimer
Réduire / Agrandir
Pour plus d'options, connectez vous !
Fiches de maths

probabilités en post-bac
1 fiches de mathématiques sur "probabilités" en post-bac disponibles.

Rechercher

Espace membre

Zone membre

Pas de compte ?
Je m'inscris

Changer d'île

Cours et Exercices de maths

Forum de maths

college

lycee

Outils de maths

Pages les plus populaires

Proba : combinaisons de 5 dés sur un seul lancer de 15 dés

Seuls les membres peuvent poster sur le forum !

Ce topic

Fiches de maths