Inscription / Connexion Nouveau Sujet
produit scalaire
bonjour, je comprends rien au produit scalaire c'est formel!
Vous pouvez m'aider avec cet éxo svp ? en fait je vois pas comment on doit s'y prendre...
A et B sont deux points tels que AB=5cm. Dans chaque cas, déterminer l'ensemble des points M vérifiant l'égalité donnée et le représenter.
a) (vecteurs) AM.AB = 20
b) (vecteurs) BM.BA = -40
Bonjour,
tout d'abord un petit résumé de cours 
un vecteur vect(AB) est défini par:
- sa direction: celle de la droite (AB).
- son sens: de A vers B.
- sa norme (sa longueur) est AB.
vecteurs colinéaires:
* 2 vecteurs non nuls vect(u) et vect(v) sont colinéaires dès qu'il existe un réel k tel que vect(u)=k*vect(v).
* Soit vect(u):(x;y) et vect(v):(x',y'), vect(u) et vect(v) sont colinéaires si et seulement si, xy'-x'y=0.
* Et d'un point de vue géométrique, 2 vecteurs sont colinéaires s'ils sont sur des droites parallèles ou s'ils sont sur une même droite.
Il n'y a pas beau coup de choses à savoir sur le produit scalaire mais il faut les savoir par coeur sinon on nage vite!
définition1: Soit u et v deux vecteurs. Si u et v sont 2 vecteurs colinéaires, alors le produit scalaire des vecteurs vect(u) et vect(v), noté vect(u).vect(v) est le nombre réel défini par (on pose vect(u)=vect(OA) et vect(v)=vect(OB):
- si vect(u) et vect(v) sont 2 vecteurs de même sens, vect(u).vect(v)= OA*OB (OA et OB sont des distances).
- si vect(u) et vect(v) sont 2 vecteurs de sens ontraie, vect(u).vect(v)= -OA*OB.
définition2: vect(u)² = vect(u).vect(u)=||vect(u)²||= OA².
définition3: Le projeté orthogonal d'un point B sur une droite D (B n'est pas sur la droite D) est le point H de D tel que les droites D et (BH) soient perpendiculaires.
Si vect(u) et vect(v) sont deux vecteurs non nuls, on définit leur produit scalaire par vect(u).vect(v)=vect(OA).vect(OH), où H est le projeté orthogonal du point B sur la droite (OA). (dessin ci dessous).
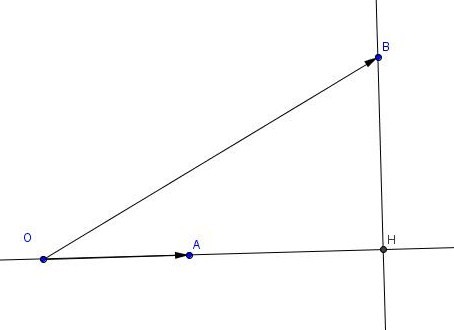
Si on reprend l'exercice:
A et B sont deux points tels que AB=5cm. Dans chaque cas, déterminer l'ensemble des points M vérifiant l'égalité donnée et le représenter.
a) (vecteurs) AM.AB = 20
 20 est posiif donc les vecteurs ont même sens, et je te laisse continuer.
20 est posiif donc les vecteurs ont même sens, et je te laisse continuer.
b) (vecteurs) BM.BA = -40


