Bonjour,

OA = 300 m  oui
DE = 1 m  oui

OD = 2 m  non  OE = 2 m
Os = 300 m  non  c'est OA

excuse-moi, (étourderie)

OB = 300 m et non pas OA

Merci  Il faut que je trouve   SA / OA / OD / OS T-T

Quelqu'un veut bien m'aider x) ?

tu n'as pas la mesure du côté de la pyramide ?
ou une autre mesure ?

Non je n'ai que celle la

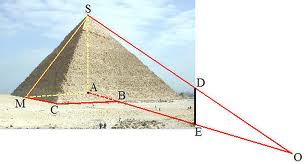
ou il faudrait que Thalès se trouve à 300 m du centre de la pyramide, ce qui n'est pas dit dans ton énoncé (?)

Nan ils dissent juste qu'il ce trouve a 300 de la pyramide ( Peut - etre du centre )
Avec ces mesures il faut trouver la hauteur de la pyramide ( SA )
Il y a aussi ecrit ''que peut tu dire de OE  OD  DE ? "
                                         _ , _ , _  
                                         OA  OS  SA

évidemment ce sont les égalités données par le théorème de Thalès appliqué aux triangles DOE et SOA
au besoin on peut calculer OD (OED est rectangle en E), mais ça s'arrête là
ou alors si OA = 300 m, on a de suite la hauteur SA de la pyramide et l'exercice est terminé !

on peut aussi calculer l'angle Ô
et donc ^EDO et ^ASO

attends, j'ai une idée

non ... j'ai essayé avec les rapports trigonométriques et ceux de Thalès -> ça tourne en rond
il manque vraiment une information

Bah merci quand même

De toute façon il faut calculer OD