Inscription / Connexion Nouveau Sujet
Triangle rectangle
Bonjours,
Est-ce que quelqu'un pourrait m'aider à faire l'exercice suivant ?
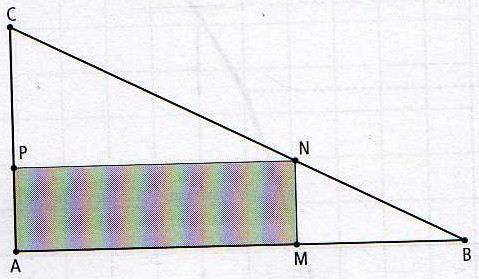
ABC est un triangle rectangle en A tel que AB = 8cm et AC = 4cm. Soit M un point du segment [AB] et AM = x.
N est un point de [BC] et P un point de [AC] tel que AMNP soit un rectangle.
Soit F la fonction qui a chaque x associe l'aire du rectangle AMNP.
Question 1: Quel est l'ensemble de définition de F ?
Question 2: Montrer que f(x) = x(8-x).
Question 3.a: Verifier que f(x) = -(x-4)2+8
Question 3.b: En déduire que l'aire du triangle AMNP est maximale pour une position particulière du point M que l'on précisera.
Bonjour,
AMNP est un rectangle  MN
MN  AP
AP
tu peux utiliser Thalès pour trouver MN:
MB/AB = MN\AC
puis l'aire du rectangle
oui c'est bien ça
attention au signe "multiplié" qui ressemble trop au "x"
dans ce cas là je préfère rien mettre
ou encore comme ça:
Et pour la question 3.a: Vérifier que f(x) = -(x-4)2+8
Moi, j'ai fait -(x-4)2+8 = -
x2-4x-4x+16+8 = -
x2-8x+24. Mais après, qu'est ce qu'il faut faire ???
après c'est la question 3b
en partant de la forme canonique:
(x-4)² est un carré toujours  0
0
-(x-4)² est toujours  0
0
je te laisse finir le raisonnement
Ah d'accord, j'ai compris, merci !!!
Au fait l'ensemble de définition de f c'est f(x)= Aire du rectangle AMNP, n'est-ce pas ?
le point M se déplace sur le segment [AB]
l'ensemble de définition c'est x  [0;8]
[0;8]
la forme canonique d'une expression (un trinôme)
c'est faire apparaitre un carré
de façon à pouvoir trouver les extrémums de la fonctions,
étudier ses variations, factoriser,...
(x-4)²  0
0
le minimum de (x-4)² est zéro pour x=4
-(x-4)²  0
0
le maximum de -(x-4)² est zéro pour x=4
-(1/2)*(x-4)² + 8
le maximum de -(1/2)(x-4)² + 8 pour x=4 est ...
-4 ? Mais, il n'y aurait pas une autre facon de pouvoir savoir pour quelle position particulière du point M, l'aire du rectangle AMNP est maximale. Parce que je crois que je n'ai pas encore étudier la forme canonique.
pour la forme canonique
tu n'es pas obligé de savoir que ça s'appelle comme ça
l'énoncé te le donne en 3a
il faut utiliser ce qu'on te donne
il suffit de savoir qu'un carré est toujours positif ou nul
l'aire sera maximale quand le carré sera nul
pour x=4
-(1/2)(x-4)² = 0
-(1/2)(x-4)² - 8 = 8
aire maximale est de 8 cm² quand x = 4 cm
le point M est au milieu de [AB] AM = 4 cm
le point P est au milieu de [AC] AP = 2 cm
aire AMNP = 4*2 = 8 cm²
Re-bonjours,
Sur le même exercice, il y a une autre question qui me gène et qui est la suivante:
Déterminer algébriquement les valeurs exactes de x pour lesquels l'aire de AMNP est égale à 4 cm2 (on justifiera que l'équation f(x)=4 équivaut à (x-4- 8)(x-4+
8)(x-4+ 8)=0).
8)=0).
Pour prouver que (x-4- 8)(x-4+
8)(x-4+ 8)=0 j'ai utilisé l'identité remarquable (a-b)(a+b)=a2+b2 c'est-à-dire que (x-4-
8)=0 j'ai utilisé l'identité remarquable (a-b)(a+b)=a2+b2 c'est-à-dire que (x-4- 8)(x-4+
8)(x-4+ 8)= (x-4)2+8
8)= (x-4)2+8
Mais après, que faut-il faire ?
l'aire du rectangle c'est -(1/2)(x-4)² + 8
pour une aire de 4 cm²
-(1/2)(x-4)² + 8 = 4
-(1/2)(x-4)² + 8 - 4 = 0
- + 4 = 0
4 - (1/2)(x-4)² = 0
différence de 2 carrés
2² - (1/2)(x-4)² = 0
2² - [(x-4)/ 2]² = 0
2]² = 0
2² - [(x-4)* 2/2]² = 0
2/2]² = 0
[2 +  2*(x-4)/2]*[2 -
2*(x-4)/2]*[2 -  2*(x-4)/2] = 0
2*(x-4)/2] = 0
[4 +  2*(x-4)]*[4 -
2*(x-4)]*[4 -  2*(x-4)] = 0
2*(x-4)] = 0
[4 2 + 2*(x-4)]*[4
2 + 2*(x-4)]*[4 2 - 2*(x-4)] = 0
2 - 2*(x-4)] = 0
[2 2 + (x-4)]*[2
2 + (x-4)]*[2 2 - (x-4)] = 0
2 - (x-4)] = 0
ouf !!!
 8 = 2
8 = 2 2
2
je l'ai prouvé sans avoir le résultat
à partir du résultat on doit pouvoir développer
et prouver que c'est bien égal à f(x)-4
( 8 + (x-4))(
8 + (x-4))( 8 - (x-4))
8 - (x-4))
8 - (x-4)² = 0
4 - 1/2*(x-4)² = 0
8 - 1/2*(x-4)² = 4

 l c'est-à-dire AM
l c'est-à-dire AM




